The Magnus Prediction Model, version 6
Estimating Individual Impact on NHL Special Teams Shot Rates
September 6, 2022, Micah Blake McCurdy, @IneffectiveMath
(This model, is the special teams version of Magnus 6. The explanation here is copied from there, with changes as appropriate.)
Introduction
I would like to be able to isolate the individual impact of a given skater on special teams shot rates from the impact of their teammates, their opponents, the scores at which they play, the zones in which they begin their shifts, the instructions of their head coach, their level of fatigue, how far away their bench is, and home-ice advantage. I have fit a regression model which provides such estimates. The most important feature of this model is that I use shot rate maps as the units of observation and thus also for the estimates themselves, permitting me to see not only what portion of a team's performance can be attributed to individual players but also detect patterns of ice usage.
Here, as throughout this article, "shot" means "unblocked shot", that is, a shot that is recorded by the NHL as either a goal, a save, or a miss (this latter category includes shots that hit the post or crossbar). I would prefer to include blocked shots also but cannot since the NHL does not record shot locations (only much less useful block locations) for blocked shots.
The most sophisticated element of Magnus is the method for estimating the marginal effect of a given player on shot rates; that is, that portion of what happens when they are on the ice that can be attributed to their individual play and not the context in which they are placed. We know that players are affected by their teammates, by their opponents, by the zones their coaches deploy them in, and by the prevailing score while they play. Thus, I try to isolate the impact of a given player on the shots which are taken and where they are taken from.
Although regression is more mathematically sophisticated than some other measures, it is in no way a "black box". As we shall see, every estimate can be broken down into its constituent pieces and scrutinized. If you are uneasy with the mathematical details but interested in the results, you should skip the "Method" section and just think of the method as like a souped-up "relative to team/teammate statistics", done properly.
Method
I use a simple linear model of the form \( Y \sim WX\beta \) where \(X\) is the design matrix, \(Y\) is a vector of observations, \(W\) is a weighting matrix, and \(\beta\) is a vector of marginals, that is, the impacts associated to each thing, independent of each other things. Each passage of 5v4 or 5v3 play with no substitutions is encoded in the model as one row; the response entry of that row in \(Y\) is the pattern of shots taken by the team with five skaters. I call such passages of play with no substitutions "stints", by analogy with the same term used in basketball research, although the presence of on-the-fly changes in hockey means that some stints can be very short. Note also that a single stint can contain within it several stoppages of play, including a variety of faceoffs, so long as the players on the ice do not change. A typical NHL season contains about a hundred thousand such special-teams stints and so our design matrix \(X\) has about that many rows.
Covariates
The columns of \(X\) correspond to all of the different features that I include in the model. There are broadly, two different types of columns. Some terms occur in pairs, one for offence, one for defence:
- Player performance estimates, two columns for each skater: one for their offensive impact on the power-play (that is, on their own team's shot rates), and one for their defensive impact on the penalty-kill (that is, on their opponent's shot rates). I do not make any attempt at modelling short-handed offence nor power-play defence.
- Coach impacts: for the head coach of each team:
- A pair for general impact (attacking/defending), meant to serve as an umbrella for the effect the coach's general-purpose instructions have on how the players on the ice choose to play. These indicators are attached to the head coach only, even though in practice some or much of special teams play is mediated by other coaches.
- Rest impacts: three rest patterns:
- Played neither last night nor the night before ("well rested");
- Did not play last night but did play the night before ("normal"); and
- Played last night but did not play the night before ("tired").
The remaining terms apply only to the offensive team:
- Score impacts: seven columns for various different scores:
- trailing by three or more,
- trailing by two,
- trailing by one,
- tied,
- leading by one,
- leading by two, and
- leading by three or more.
- Zone impacts: four columns for the zones in which attacking players start
their shifts. The four "shift start types" that I use are:
- Offensive Zone,
- Neutral Zone,
- Defensive Zone, and
- On the fly.
- Game Time and Venue: six columns indicating if the attacking players are the
home or the road team and which period the stint is in:
- Home Team 1st Period,
- Home Team 2nd Period,
- Home Team 3rd Period,
- Away Team 1st Period,
- Away Team 2nd Period,
- Away Team 3rd Period,
Response
The entries in \(Y\), the "responses" of the regression, are functions which encode the rate at which unblocked shots are generated from various parts of the ice. An unblocked shots with NHL-recorded location of \((x,y)\) is encoded as a two-dimensional gaussian centred at that point with width (standard deviation) of ten feet; this arbitrary figure is chosen because it is large enough to dominate the measurement error typically observed by comparing video observations with NHL-recorded locations and also produces suitable smooth estimates.
By controlling for score, zone, teammates, and opponents in this way, I obtain estimates of each players individual isolated impact on shot generation and shot suppression.
Fitting
To fit a simple model such as \(Y = WX\beta \) using ordinary least squares fitting is to find the \(\beta\) which minimizes the total error $$ (Y - X\beta)^TW(Y - X\beta) $$ Since \(X\beta\) is the vector of model-predicted results (where \(\beta\) "is" the model), the difference between it and the observed results \(Y\) is a measure of error; forming the weighted product of \(Y-X\beta\) with itself is squaring this error (to ensure it's positive), and then we want to minimize this total error: hence the name "least squares".
When the entries of \(Y\) are numbers, this error expression is a one-by-one matrix which I naturally identify with the single number it contains, and I can find the \(\beta\) which minimizes it by the usual methods of matrix differentiation. To extend this framework to our situation, where the elements of \(Y\) are shot maps, I use a dissection of the half-rink into ten-thousand pieces, as a hundred-by-hundred grid. This divides the rink up into parcels one foot long by 0.85 feet wide, sufficiently coarse to permit efficient computation and sufficiently fine to appear smooth when results are gathered together. In particular, since the input shot data is smoothed into sums of gaussians before the regression is fit, we can compute the regression as if it were ten thousand separate regressions whose outputs are combined to form the maps for each term. It might be helpful to imagine a video broadcasting system, where input video is spliced into channels, each channel modified by appropriate filters for the display media at hand, and then each channel organized into an output which viewers can percieve as a single object. The practical benefit of this is that I can use the well-known formula for the \(\beta\) which minimizes this error, namely $$ \beta = (X^TX)^{-1}X^TWY $$ which makes it clear that the units of \(\beta\) are the same as those of \(Y\); that is, if I put shot rate maps in, I will get shot rate maps out.
However, I choose not to fit this model with ordinary least-squares, preferring instead to use generalized ridge regression; that is, instead of minimizing $$ (Y - X\beta)^TW(Y - X\beta) $$ as in ordinary least squares, I add three so-called ridge penalties, to instead minimize: $$ (Y - X\beta)^TW(Y - X\beta) + (\beta-\beta_0)^T \Lambda (\beta - \beta_0) + \beta^T K \beta $$ Each ridge penalty has the same structure; the first term says that deviation of the model (that is, \(\beta\)) from the data is bad; the second term says that deviation of the model from the specified vector \(\beta_0\) of priors is bad, and the matrix \(\Lambda\) controls how "bad" such deviation is to be considered. The two matrixes we use here (\(\Lambda\) and \(K\) are how we we specify our prior beliefs about the things being modelled, after we know what the circumstances are but before we consider the response data itself.
The historical penalty
Although the exposition here focusses on 2021-2022, the most-recent season of NHL hockey as I write this, in practice I fit this model successively, first on 2007-2008, the first season for which the NHL provides data at this level of detail, and then repeating the process for all subsequent seasons. Thus, after each season, I have a suite of estimates of player ability which I do not throw away. Since I am trying to estimate player ability (not performance), I take the opinion that our estimates ought to change slowly, since a player's athletic ability also usually changes slowly. Furthermore, the game of hockey itself also changes (that is, its rules change, and also teams in the aggregate choose their players and playstyles differently) but does so slowly. Thus, every term in the model is biased towards its value from the previous season. This is done by taking \(\beta_0\) to be the \(\beta\) from the previous season, and populating the diagonal elements of \(\Lambda\) itself with the estimated precisions from the previous season.
In my 5v5 model, I bias players with no experience towards a point somewhat weaker than average; but for special teams work I use league average instead.
In 2007-2008, with no prior year of data to guide me, I use the zero vector instead, with a suitably broad uncertainty.
The regularization penalties
The normal penalty
The next two penalty terms encode our prior knowledge about the NHL specifically, about the overall quality of the players and coaches in it. In addition to returning players individually, we know that players who play in the league are selected; they have been drafted or signed from other leagues; every one of them has a substantial body of work examined by their managers and coaches, in one way or another. Furthermore, the athletic abilities themselves which we are primarily interested in are constrained, very generally, by what we know about the possibilities of human performance, and ultimately by physics itself. In particular, this means that extreme estimates are unlikely for this reason, regardless of the happenstances of any on-ice observations. Thus, we impose a penalty on every skater towards "NHL average". This is the "usual" ridge penalty, \( (\beta-\beta_K)^T K (\beta-\beta_K)\), where \(\beta_K\) is conveniently the zero vector, since "league average" each season is the reference point we choose to use for our regression.
A truly disciplined modeller would have used the league average from the previous year, in order to maintain faithful observance of using only prior data in specifying the prior, but I have cheated slightly and used the data from the season at hand instead. I crave the reader's forgiveness.
The strength of the penalty is encoded into the diagonal entries of \(K\) as follows:- For the score columns, the zone columns, the rest columns, the long change term, and the home-ice intercept, I choose a value of 0. These terms are not theoretically constrained, and the fitting in this region of the model is like ordinary-least-squares fitting.
- For coaching and player terms, I use a value in \(K\) of 10,000. Choosing this value is somewhat ad hoc; but does produce stable, slowly varying estimates. More involved theoretical estimates of optimal penalty values (such as computing the generalized cross-validation error, following Brian MacDonald (Section 5.3)) suggest much smaller values which give wildly varying (and hence unworkable) year-to-year estimates of player ability.
- Rookies or other players with low icetimes are not treated differently in any way, unlike in the first version of Magnus.
Players that we expect before we see their on-ice results or circumstances to be of similar ability can be fused, that is, penalty terms can be introduced to encode our prior belief that they are similar. I have chosen to fuse the Sedins in this way, with a penalty term of weight 10,000, because they are twins. I don't consider any more-distant relation than twins as legitimate grounds for this kind of prior.
Pooling penalties
Finally, I apply a set of penalties to encode prior knowledge about how the various structural terms are distributed, so that certain sets of terms can be "pooled" properly. For example; whatever the particulars of who starts which shifts in which zones, we expect that the total impact of zone starts on the entire league over a season to be zero, since every effect that helps one team should have a matching effect hurting their opponents. In previous iterations of this model I have worked around this by using one shift-start state (on-the-fly) as the "reference" state, thus having no model term, and then using indicators variables for the others (neutral zone, defensive zone, and offensive zone). However, this is a shade clumsy, requiring us to understand every term as "change from an on-the-fly shift", rather than, as I would strongly prefer, as "change from average".
Generally, if there are terms \(a_k\) in a model and we have weights \(w_k\) and would like to enforce $$ \sum_{k} w_ka_k = 0 $$ it suffices to ask that the square of \((\sum w_ka_k)^2\) should be small; expanding the square and interpeting the coefficients of each \(a_ia_j\) as the element \(K_{ij}\) of the penalty matrix \(K\) does the trick.
So, after forming the design matrix \(X\), but before considering the on-ice results \(Y\), we can obtain the relevant weights \(w_k\) with which to encode our prior expectation that shift-start terms should be, in aggregate, zero-sum.
For instance, if \(i\) is the index for the neutral zone term, and 17.5% of shifts in a given season begin in the neutral zone; and \(j\) is the index for on-the-fly starts, and 60.5% of shifts in a given season begin on-the-fly; then \(K_{ij}\) is set to the product of 17.5% with 60.5%; similarly with every ordered pair of zone terms to give sixteen non-zero entries in \(K\).
In the same way, we enforce that:
- The score terms should (weighted) sum to zero;
- The rest terms should sum to zero;
- The six "structure" (period and home/away) terms should sum to zero;
- All of the coaching terms for all of the teams taken together should sum to zero;
All of these pooling penalties are multiplied by an extremely strong factor (a million times larger than the 10,000 penalty for the coaches and players above). Deviation from average for players or coaches is increasingly unlikely (but not impossible) as the deviation grows; here deviations from the desired sums are contradictions in terms.
The model can be fit to any length of time; in this article I'll be describing the results of fitting it iteratively on each season from 2007-2008 through 2021-2022 in turn. For 2007-2008, we use "NHL average"; for later seasons I use the estimate from the previous season as the prior for each column, when present.
Computational Details
So, after all that, the thing we would like to put our impatient hands on is the vector \(\beta\) which minimizes the following expression: $$ (Y - X\beta)^TW(Y - X\beta) + (\beta-\beta_0)^T \Lambda (\beta - \beta_0) + \beta^T K \beta $$
Happily, the usual methods (that is, differentiating with respect to \(\beta\) to find the unique minimum of the error expression) gives a closed form for \(\beta\) as: $$ \beta = (X^TWX + \Lambda + K)^{-1}(X^TW Y + \Lambda \beta_0 ) $$ In effect, instead of assuming every season that the league is full of new players about whom we know nothing, we use all of the information from the last dozen years, implicitly weighted as seasons pass to prefer newer information without ever discarding old information entirely.
Persnickety folks, who might wonder if there really is a unique minimum to the complicated error expression we wish to minimize, may rest assured that it suffices for all of the penalty matrixes \(\Lambda\) and \(R\) to both be positive semi-definite, which they are, as motivated readers may verify at their leisure. (For the etymologically and historically curious, ridge regression was invented in the first place by folks who were interested in solving problems where the matrix \(X^TWX\) was not invertible because a certain subspace of the columns of \(X\) was "too flat" in some quasi-technical sense. The artificial inserted matrix \(\Lambda\) adds a "ridge" in this notional geometry and makes the sum \(X^TWX + \Lambda\) conveniently invertible. The Bayesian "prior" interpretation, so important to my approach here, was discovered somewhat later.)
Results
Game State
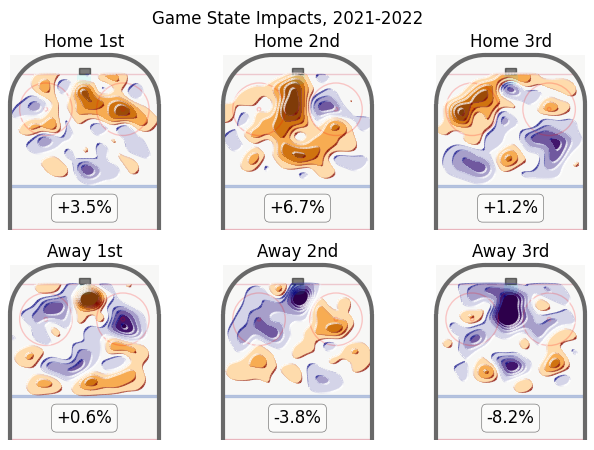
Every column in the regression corresponds to a map of shot rates over a half-rink. The simplest are perhaps the six "game state" terms:
Unsurprisingly, the home team has an advantage in each period, while the second period shows an uptick in shot danger for both teams. Perhaps more surprisingly, the third period shows a decrease in shots for both teams relative to the first period, even after accounting for score effects.
All of the maps are depicted here are to be understood as relative to league average expected goals for the season in question. Regions in red show more-and-more-dangerous shots coming from a given region of the ice than average, and blue regions show fewer-and-less-dangerous shot patterns than average. White regions see shot patterns that are roughly as dangerous as average. A full explanation of this expected goals model can be found here and the cleverness required to encode xG rates in pictures here.
For convenience, the xG rate of the term, relative to baseline PP xG rate, is also shown in the neutral zone. So, displayed above, the effect on shots to being the home team in the second period +9.8% xG/60, which means that simply being the home team (in addition to any benefit gained by matchups) is associated with generating a pattern of shots likely to result in 9.8% more goals per hour than league average, given average shooting and goaltending talent.
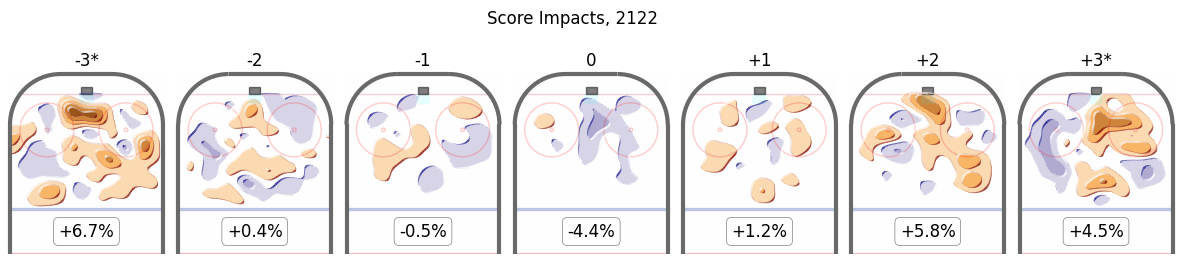
Score
The six score terms are as follows:
On special teams the well-established even-strength pattern (trailing teams dominate play, even though they still usually lose) is much less clear. This season as in some but not all previous seasons, the tendancy is for power-plays to be timid when tied.Fatigue
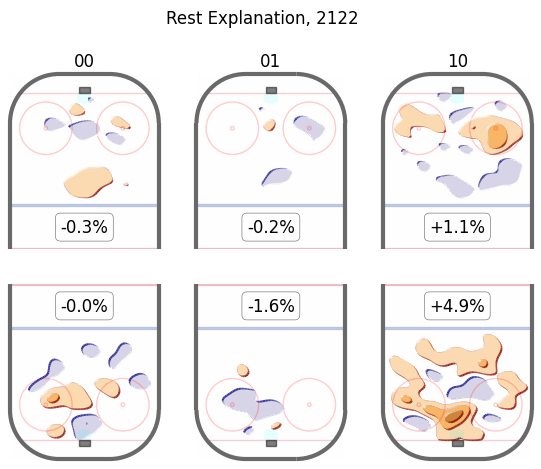
The fatigue terms are as follows, where '01' is "normal" (played the night before last but not last night), '00' is "well rested" (played neither night) and '10' is "tired" (played the night before).
Comparatively, the effects of fatigue from previous games on power-plays are quite small, relative to the effects of fatigue on the penalty-kill.
Zone
The three zone terms are as follows:
The pooling penalties permit us to compare all of the zone starts to one another directly. As expected, starting in the offensive zone helps boost shot rates considerably, and starting in your own zone depresses your shot rates even more. On-the-fly changes have a milder negative effect; such changes during special-teams play are much less common than at 5v5, where they have a positive effect instead.
Distributions
One obvious reason to construct such a model is to suss out the abilities of players, which is intrinsically interesting. However, we can also make comparisons about how much each of the various factors in our models affect play.
"Raw" on-ice results
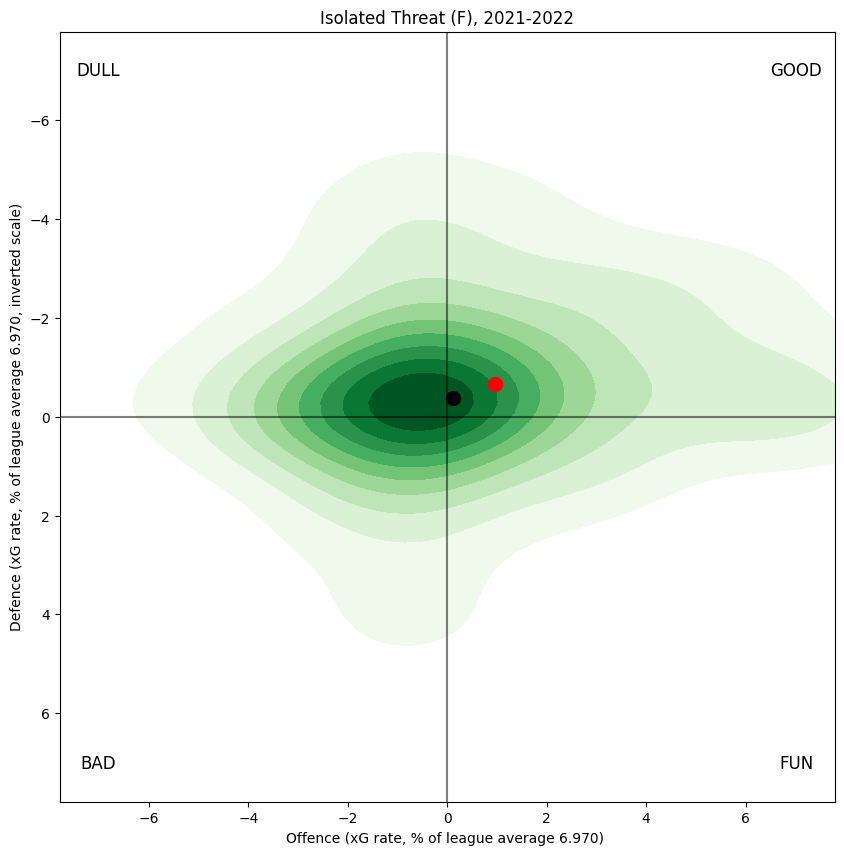
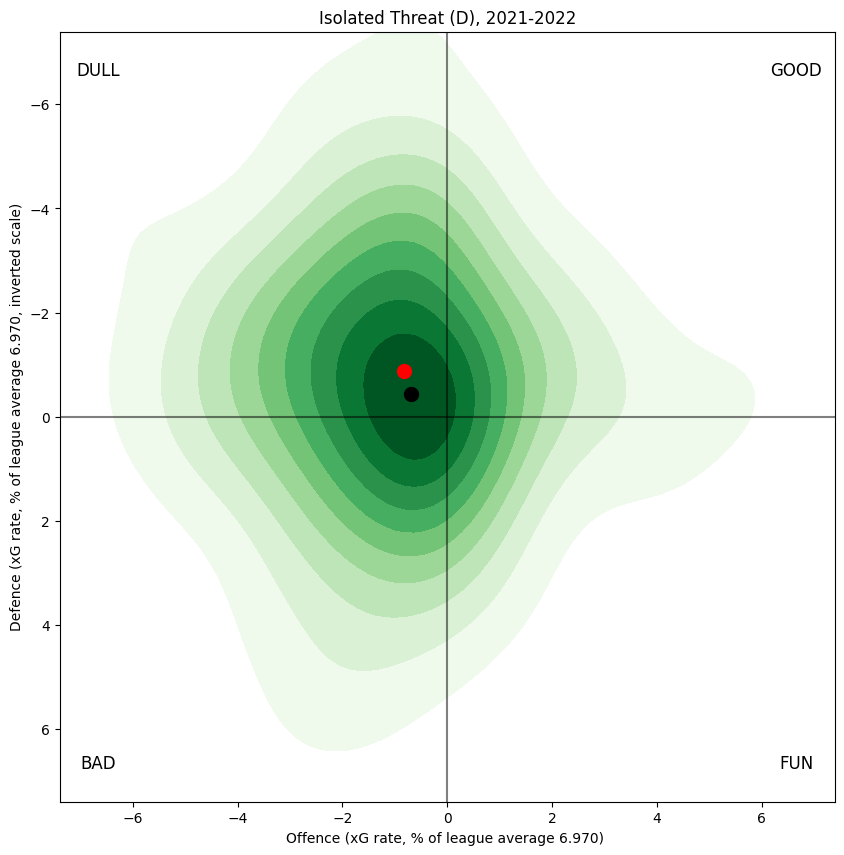
Before I describe the model outputs, I turn first to the raw observed results from the 2021-2022 regular season.
This graph is constructed as follows: for every skater who played any special teams minutes, compute the xG created and allowed by their team while they were on the ice; this produces a point \((x,y)\). Then, form the density map of all such points, where each point is weighted by the corresponding number of minutes played by the player in question. For ease of interpretation, I've scaled the xG values by league average, so that a value of \((5,5)\) on the graph means "threating to score 5% more than league average, and also threatening to be scored on 5% more than league average". As is my entrenched habit, the defensive axis is inverted, so results that are favourable to the skater in question appear in the top right (marked "GOOD" so that there can be no doubt). The contours are chosen so that ten percent of the point mass is in the darkest region, another ten percent in the next region, and so on. The final ten percent of the point mass is in the white region surrounding the shaded part of the graph. For convenience the weighted sum of the values is marked with a red dot; this dot represents the centre of the mass of the distribution, on which you could balance the whole shooting match on the tip of your steady fingertip.
Player Marginals
Repeating the above process with the individual player marginal estimates gives the following graph in green. The overall shape is still broadly normal, but the spread in power-play impact is considerably broader than the spread in penalty-kill impact.
One guiding principle of mine is that I don't include any terms in the model itself that identify players by position, since I would like to be able to measure differences between positions. With that in mind, here is the same density as above, but only for forwards:
Forwards
and again for defenders:Defenders
Not surprisingly, forwards generate somewhat more offence, on average.
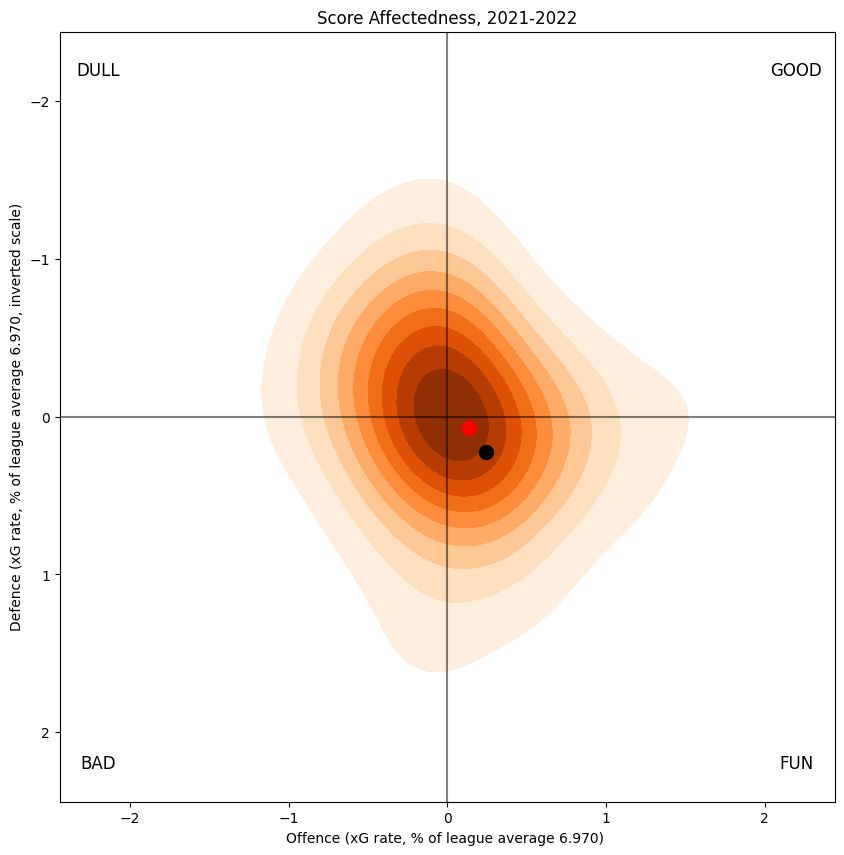
Score Impact
Zone Impact
Coach Impact
Since coaches change and players change teams, and players do not play in every score state equally, not every player is affected by coaching systems the same amount. That said, there are only around thirty-five or forty head coaches in the league each year, so the distribution of coaching effects on players is lumpier.
The above shows the impact on players due to coaches. To see the "overall" coach terms specifically, I've condensed them here:
It is not clear to me why good power-play sytems seem to be (moderately) correlated with good penalty-kill systems, but that is what we see.
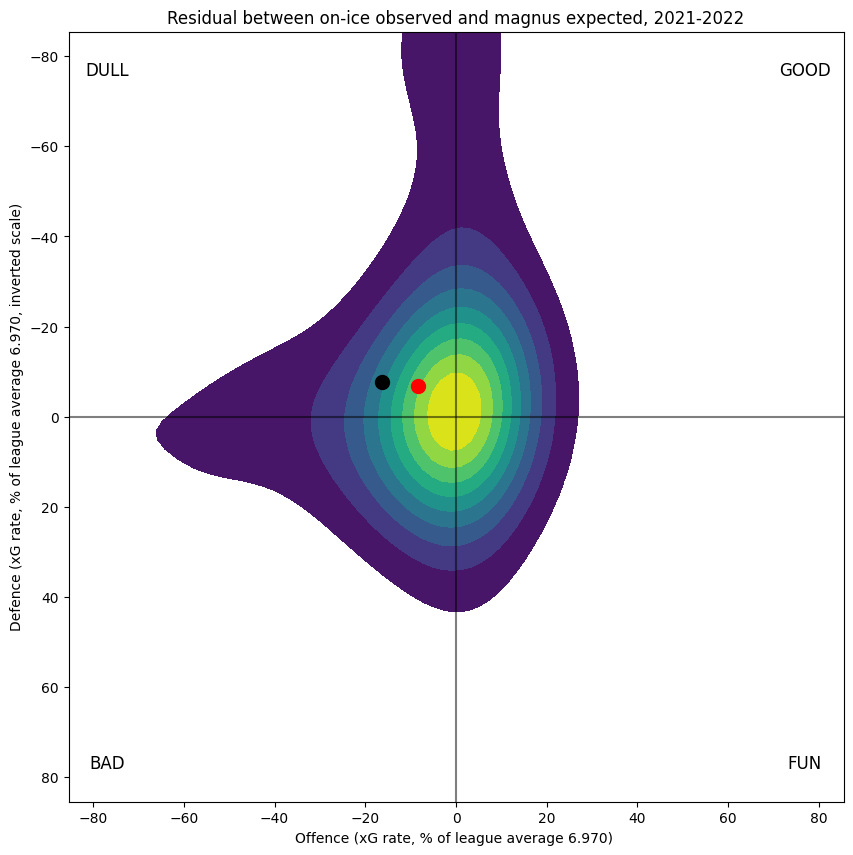
"Residuals"
Strictly speaking, residuals for a regression refer to the differences between the individual observations (that is, each stint) and the predicted shot rates for that stint. As a perhaps more insightful alternative, for each player, I can compute the difference between their raw (observed) special-teams on-ice results and what I would expect from computing the model outputs associated with the observed players and the zones and scores and home-ice advantage they player under. This is shown below:
This makes a sort of "goodness of fit" measure. The obviously circular shape is encouraging; the skew towards "dull" is caused by a number of players who have substantial minutes at one of power-play or penalty-kill but very few (often none) at the other.
Previous Work and Acknowledgements
Using zero-biased (also known as "regularized") regression in sports has a long history; the first application to hockey that I know of is the work of Brian MacDonald in 2012. His paper notes many earlier applications in basketball, for those who are curious about history; also I am very grateful for many useful conversations with Brian during the preparation of the first version of Magnus. Shortly after MacDonald's article followed a somewhat more ambitious effort from Michael Schuckers and James Curro, using a similar approach. Persons interested in the older history of such models will be delighted to read the extensive references in both of those papers.
More recently, regularized regression has been the foundation of WAR stats from both Emmanuel Perry and Josh and Luke Younggren, who publish their results at Corsica (now sadly defunct) and Evolving-Hockey, respectively.
Finally, I am very thankful to Luke Peristy for many helpful discussions, and to the generalized ridge regression lecture notes of Wessel N. van Wieringen which were both of immense value to me.
As far as I can tell, the extension of ridge regression to functions (that is, shot maps instead of just single numbers) is new, at least in this context.