2018-2019 Regular Season Retrospective

April 26, 2019, Micah Blake McCurdy, @IneffectiveMath

Some exposition here is copied from my 2016-2017 Retrospective

Various people have made models to try to predict the outcomes of hockey games, including me. I think the problem is intrinsically interesting, and I find it helpful as a point around which to organize much of my work in hockey. A good model has many aspects, chiefly:

• Sensible methods which give insight into the processes being modelled;
• Interpretability of inputs and outputs; and
• Suitably accurate and precise results.

This article is about the last item.

The models under consideration here are:

• My model, Magnus, published on this site,
• Peter Tanner's model, published at Moneypuck.com,
• Dominik Luszcyzszyn's model, published on his twitter account @domluszczyszyn,
• Harry Shomer's model, published on his twitter account @36hobbit,
• Matt Chernos's model, published on his twitter account @mchernos,
• Matt Barlowe's model, published on his twitter account @barloweanalytics,

For models that output probabilities, there is no sensible way to say that a model is "right" or "wrong", such binary judgments apply to binary choices which these models do not make. Instead, I use using "logarithmic loss", that is, assigning a score of -ln p to an event which occurs and which was predicted to occur with probability p. This loss function is called "logarithmic" because it is defined with the natural logarithm function (ln) and is is commonly abbreviate to "log-loss". I like log-loss best because it is the only scoring rule which, if the people estimating the probabilities know that it will used ahead of time to judge them, incentivizes them to quote probabilities which exactly match their certainty of the events in question occurring.

The obvious benchmark for a model of probability is to simply say that the home team has a 50% chance of winning every game, this gives a log-loss of -ln 0.5 ≈ 0.693. A supremely confident prediction that a team will win with a chance of 99% gives a log-loss, if correct, of -ln 0.99 ≈ 0.01, and if incorrect, of -ln 0.01 ≈ 4.605. Scores close to 0 are "not at all wrong", and high scores are "very wrong". However, the benchmark value of 0.693 is not one that sticks in the mind and the lower scores being better is confusing. In an effort to make log-losses more understandable, I apply a linear scaling to map 0.693 to 50 and 0 to 100. This makes log-loss behave like a test score - fifty is the passing grade, and a hundred is a perfect score. However, unlike test scores, models with extremely bad predictions can score below zero (and one or two games from one or two models this year did score below zero). I call this "log-loss-as-test-score", for lack of a better name; and every prediction is its own little test, graded by the outcome of the game.

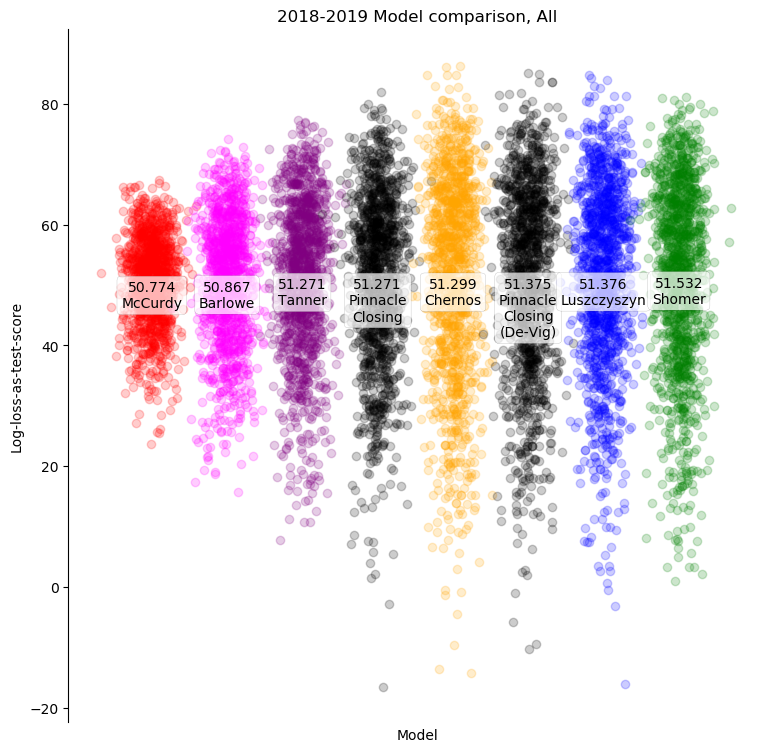
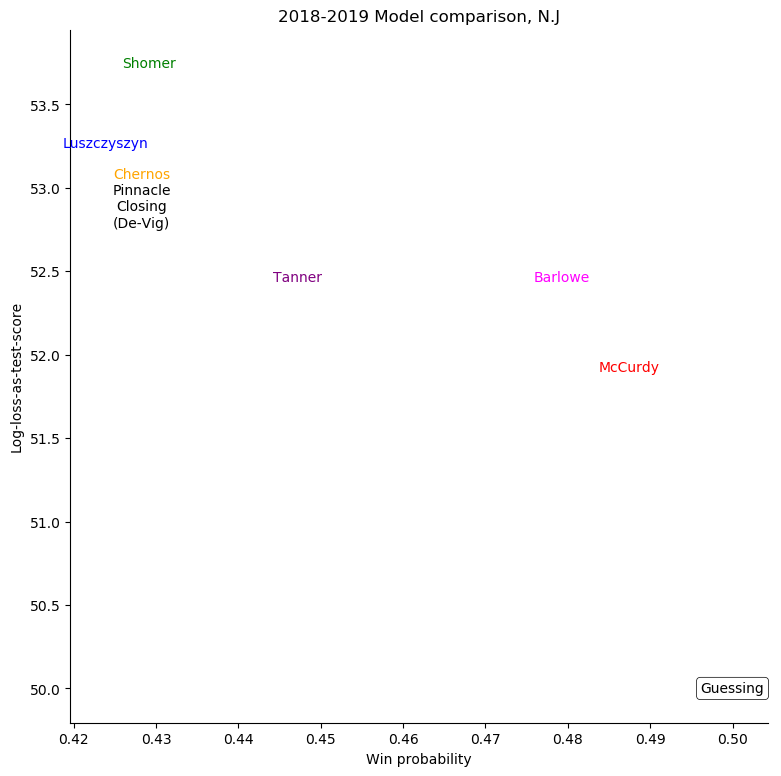
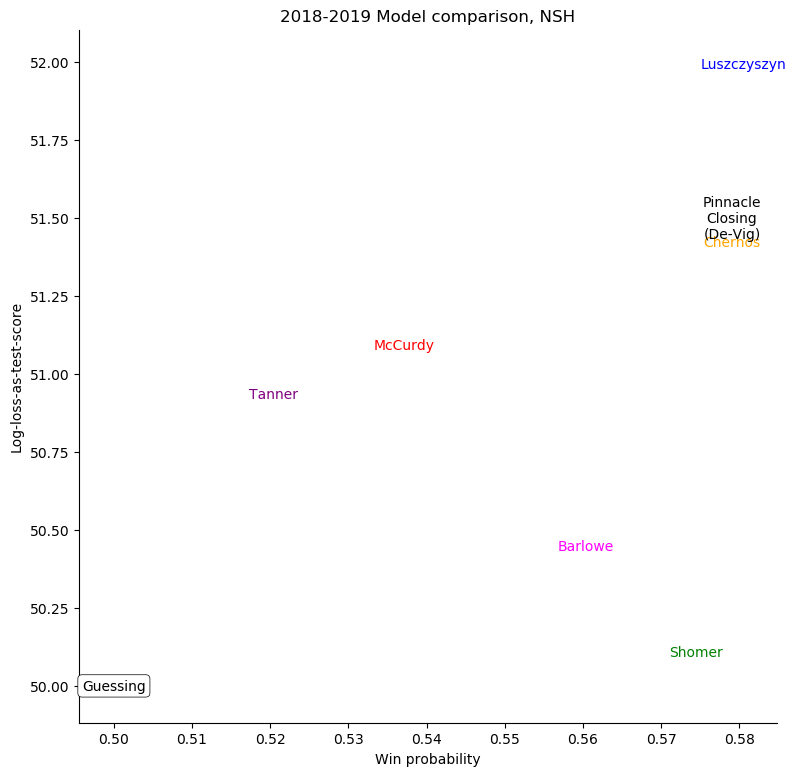
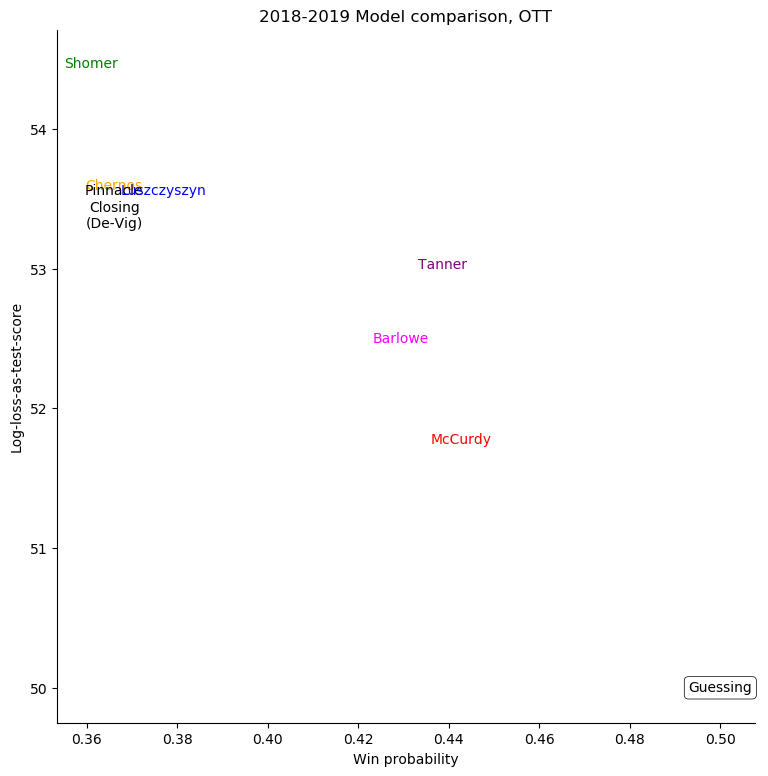
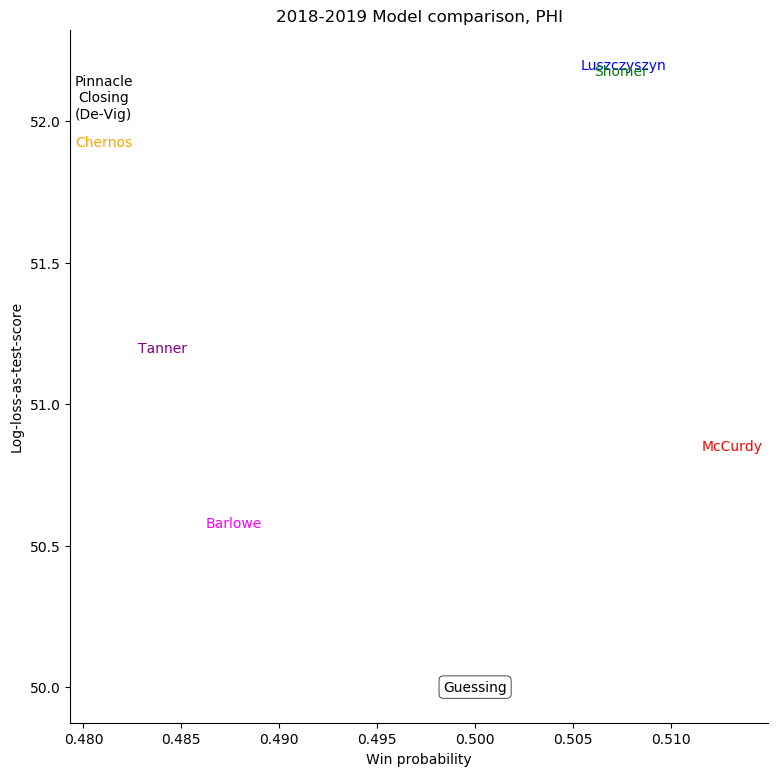
Each point displayed is an individual game of the 2018-2019 season, with its log-loss-as-test-score for each model. Most obviously, every model is very slightly better than the guessing benchmark of 50 points, and the differences between models in overall performance is extremely slight. More interestingly, despite the overall similarities in results, each model has a considerable spread in results. Some models, like mine and Matt Barlowe's, are by nature conservative, assigning probabilities close to 50%. Others, like Harry Shomer's and Dominik Luszczyszyn's, are more extravagant, assigning probabilities far from 50%.

For a more difficult task than simply out-peforming a person guessing, I've also included probabilities corresponding to Pinnacle closing lines, as well as the "true" probabilities implied by those lines after removing the price of placing wagers. These probabilities are generated by a combination of models (which are used to set opening lines) and the wagers of the public before the lines close. The models involved are obviously private but form a useful comparison nevertheless.

Deciles of Risk

Another way to assess prediction models of this type is by computing so-called "deciles of risk", that is, sorting all of the output probabilities for each model from lowest to highest, binning them into ten bins, and comparing the predicted probabilities for each bin to the proportion of home team wins in each bin.
For models without structural defects, these differences should be randomly distributed around zero, as they seem to be for most or perhaps all models considered here. (Astute (not to say pedantic) observers will have noticed that the 2018-2019 regular season contains 1271 games, which is not divisible by ten; I deleted the game with median probability from each model's list of predictions so that I could divide 1270 into ten bins of 127.)

Probability vs Log-loss

To see just where individual models went wrong, it's helpful to consider a set of teams and compare the probabilities given to the log-losses for those teams. First of all, we can consider all home-teams:
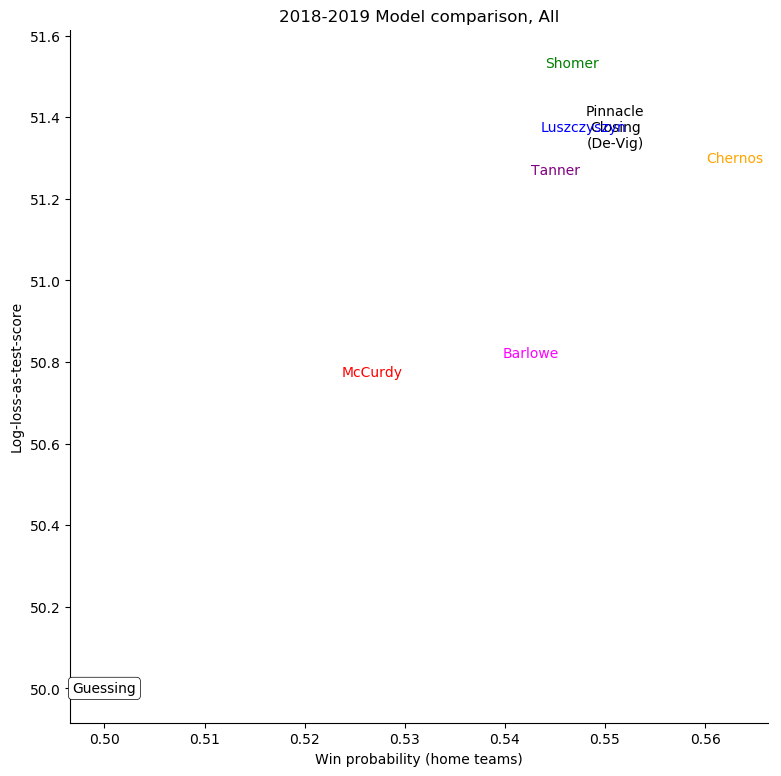
One difference that emerges is that my model is much less sanguine about the benefits of home-ice advantage than all of the others. It's not clear that this is a defect or a strength in itself, though; since some models which have stronger home-ice advantage have better results and others worse.

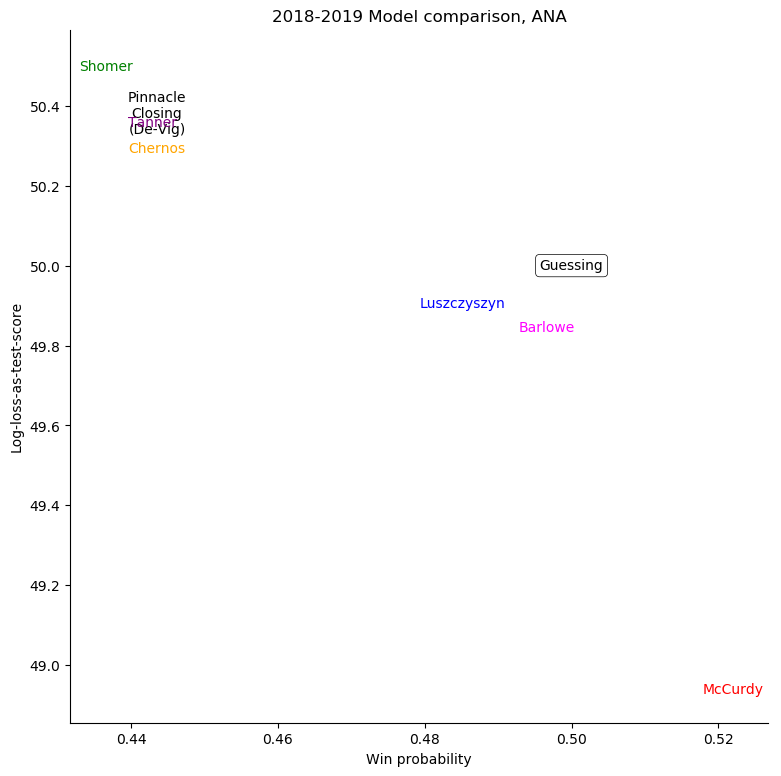
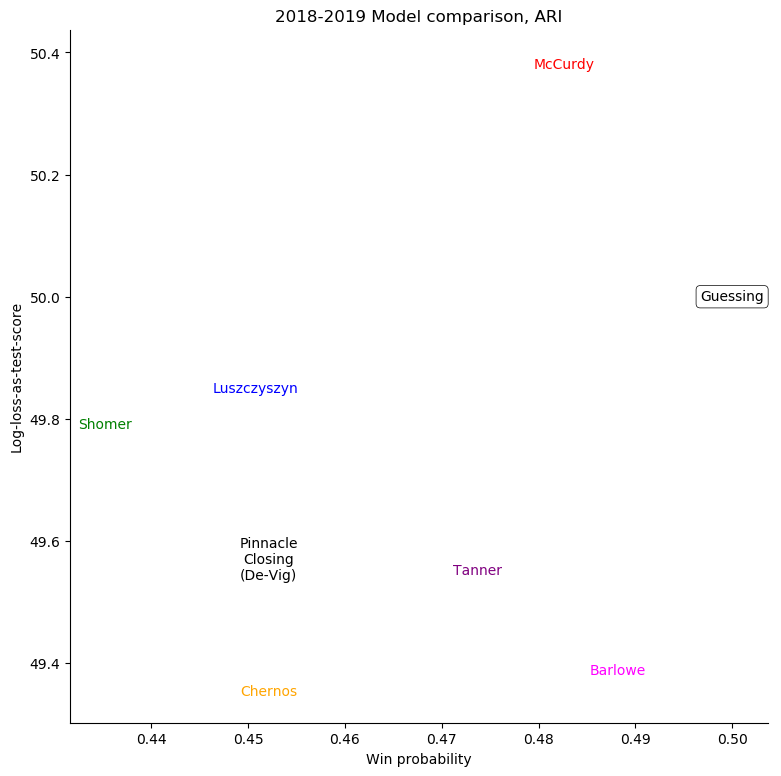
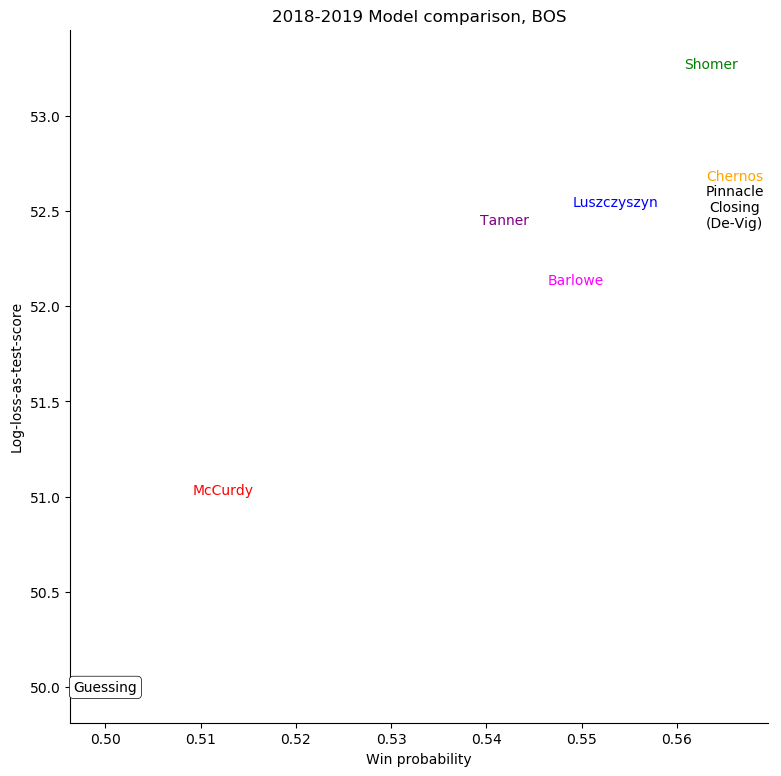
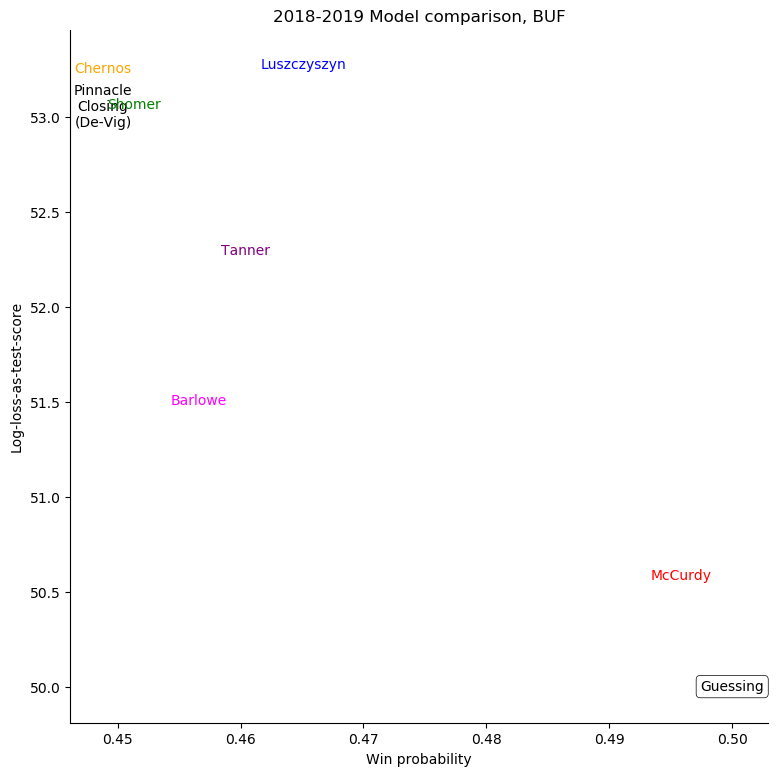
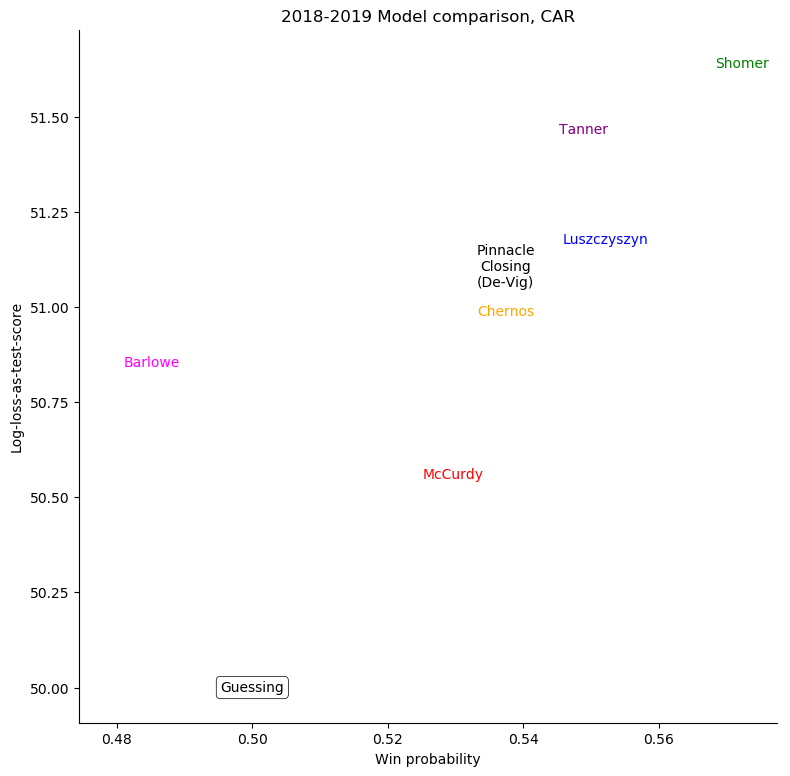
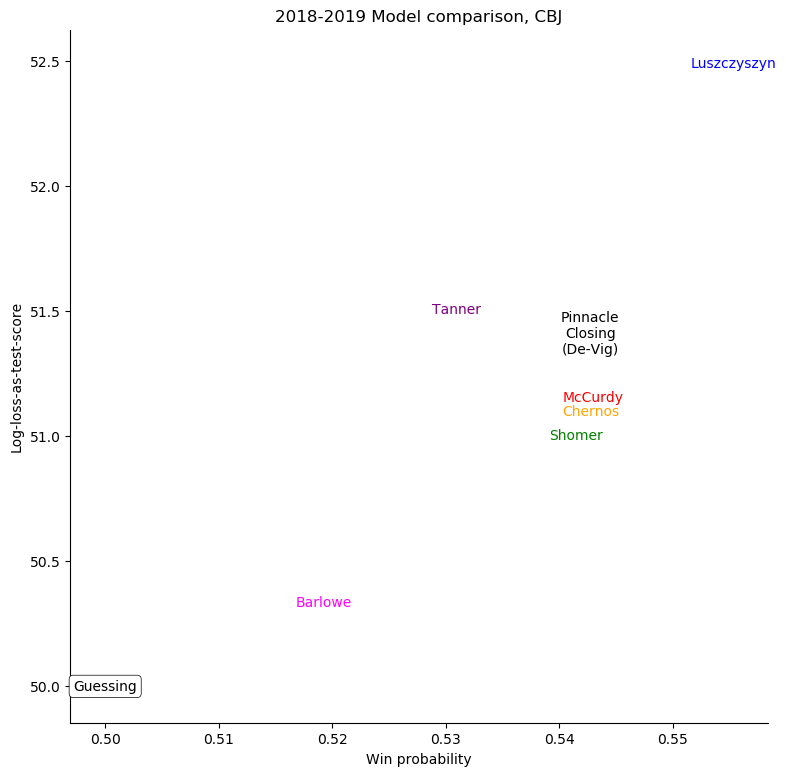
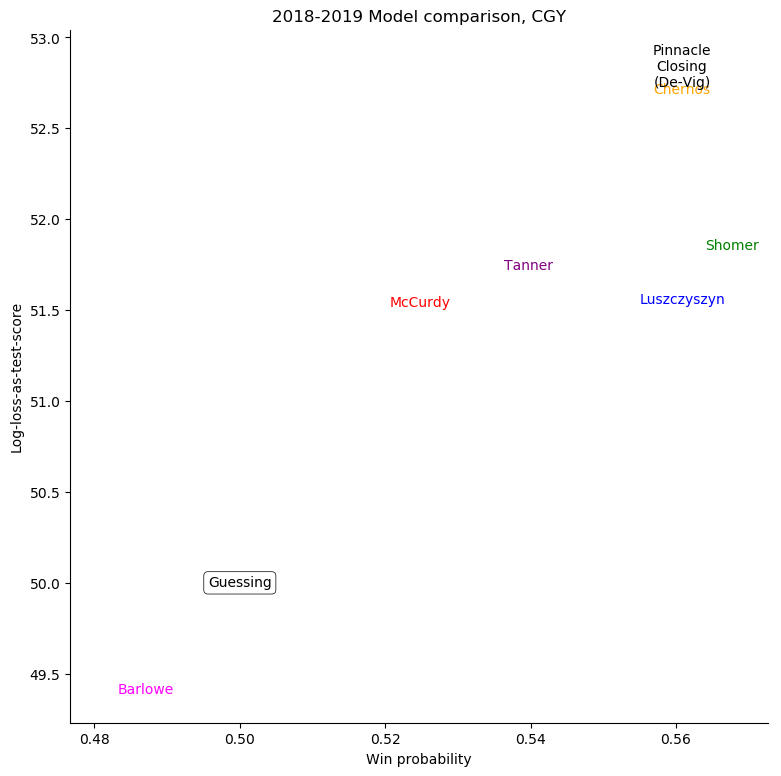
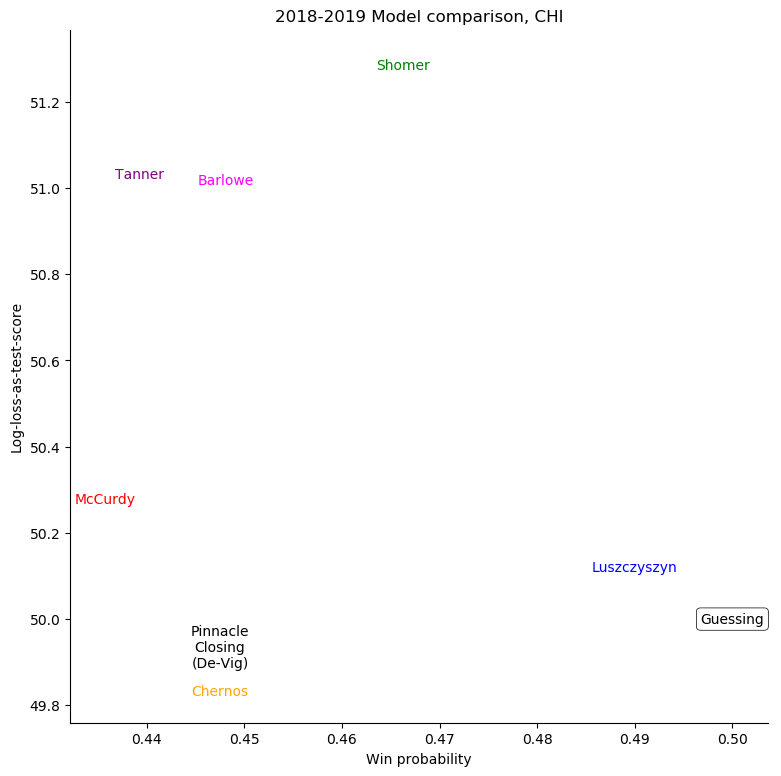
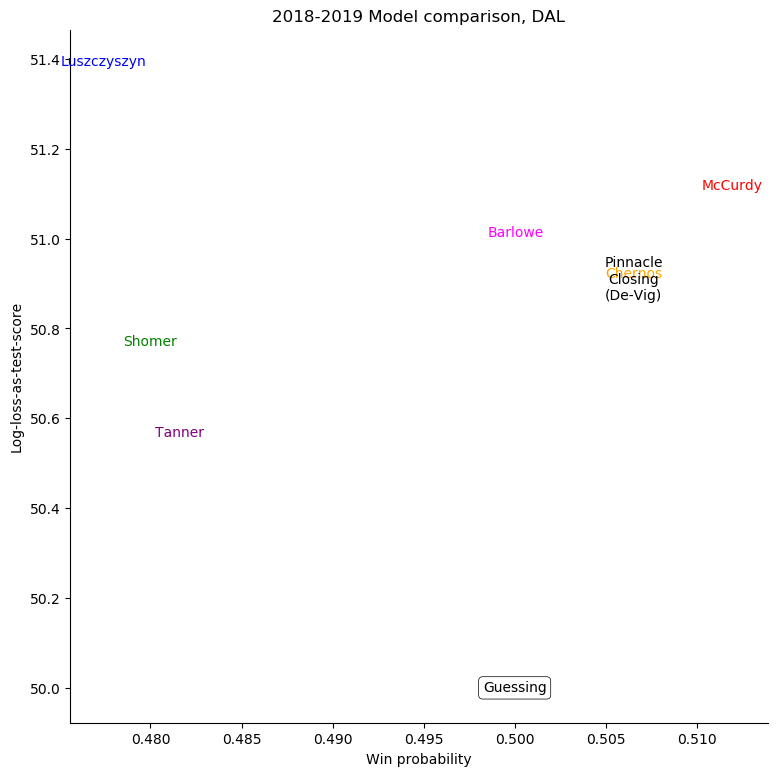
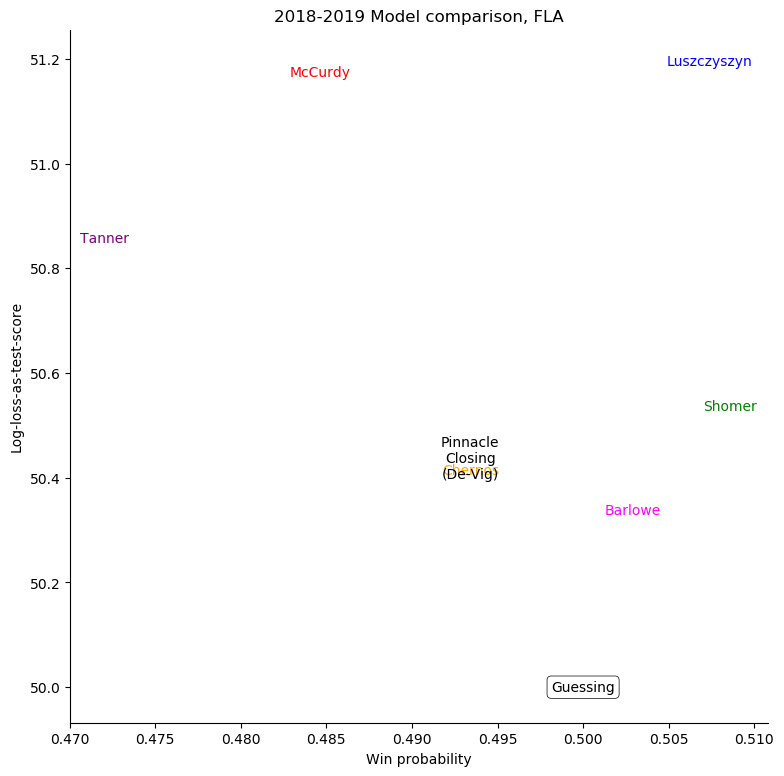
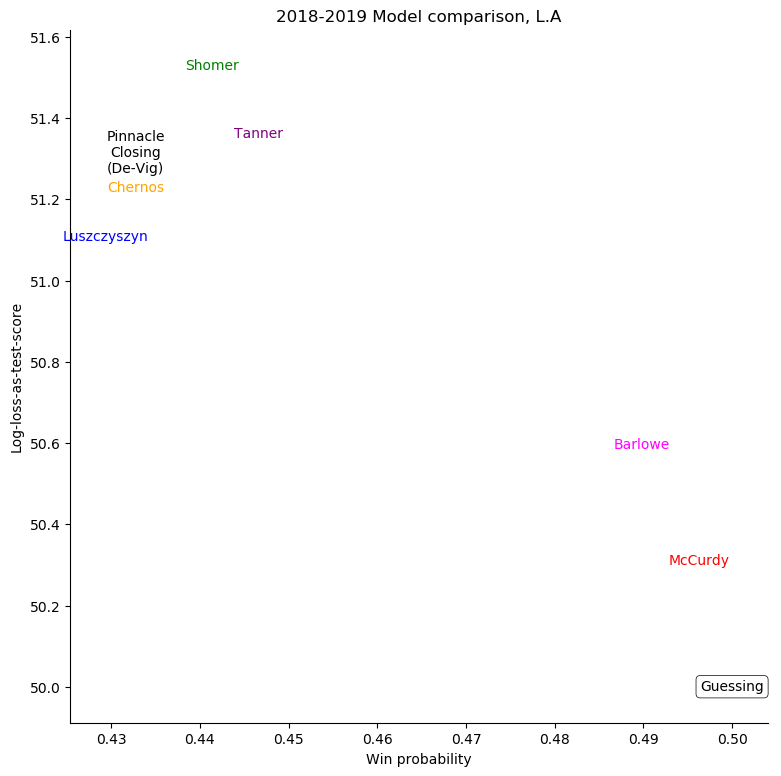
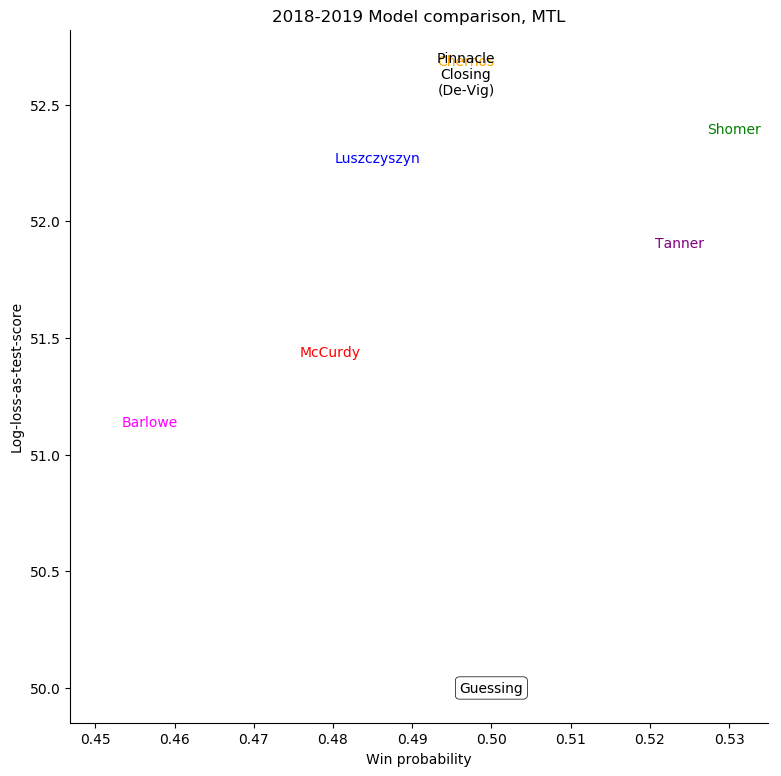
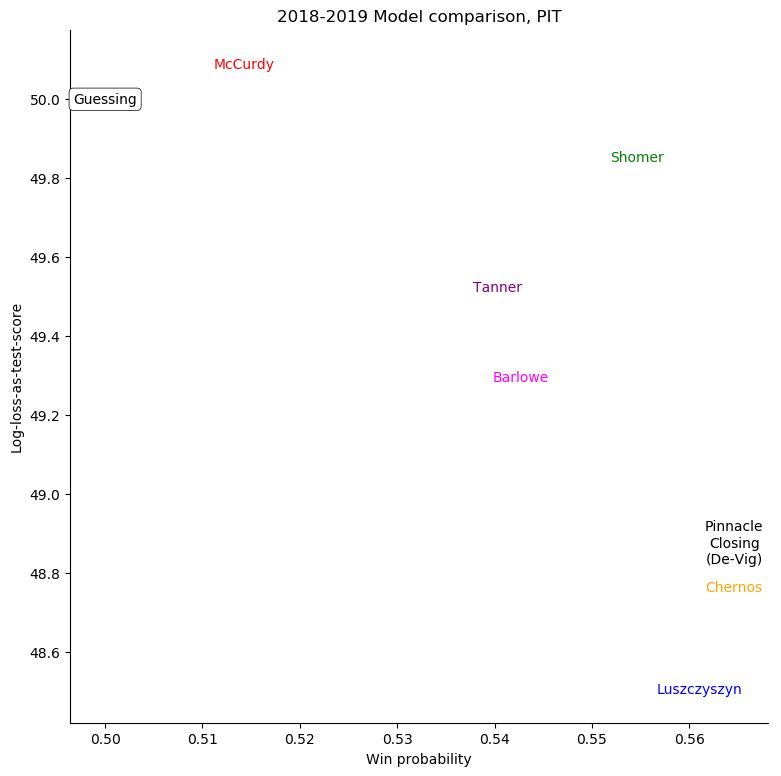
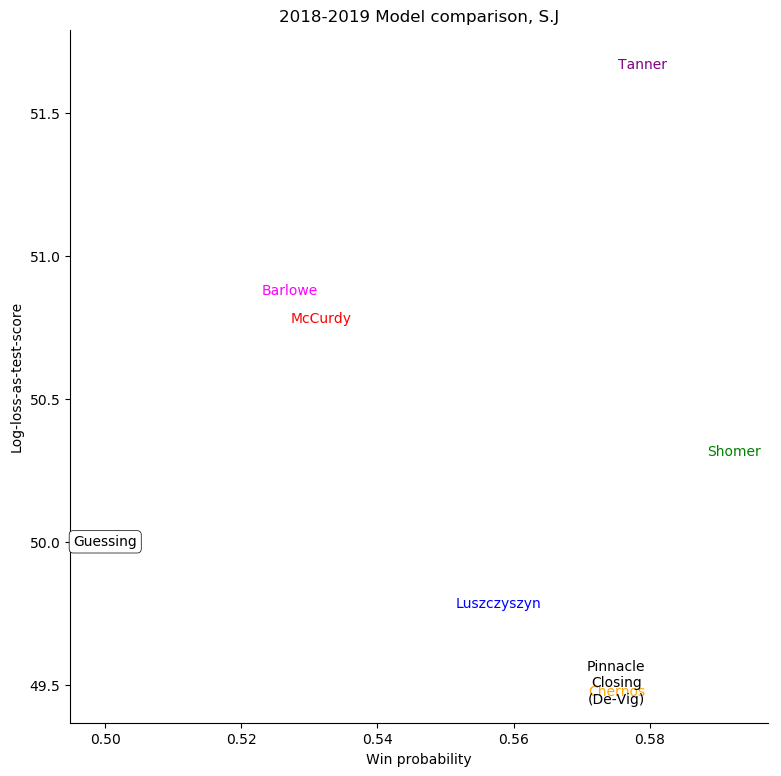
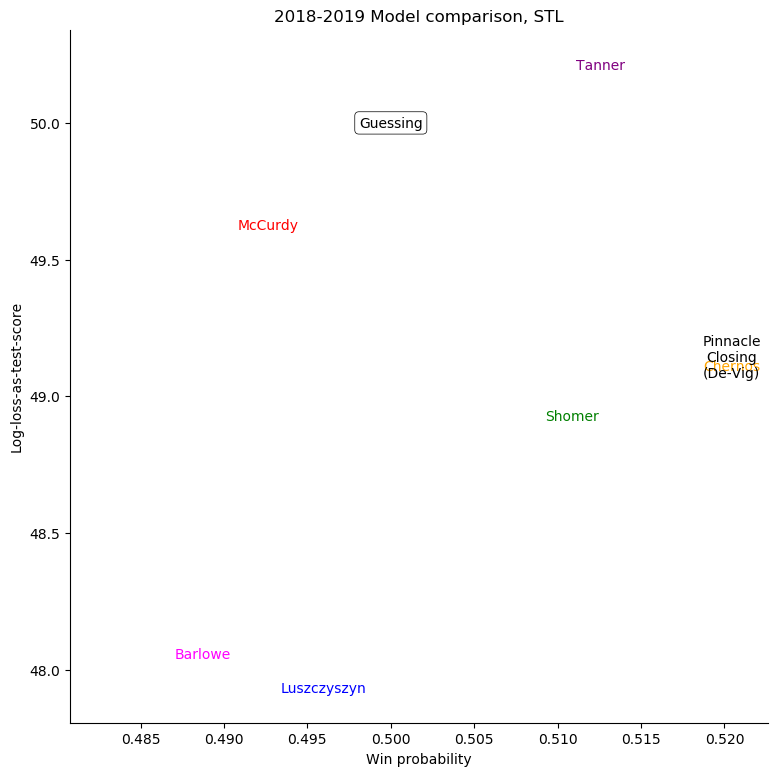
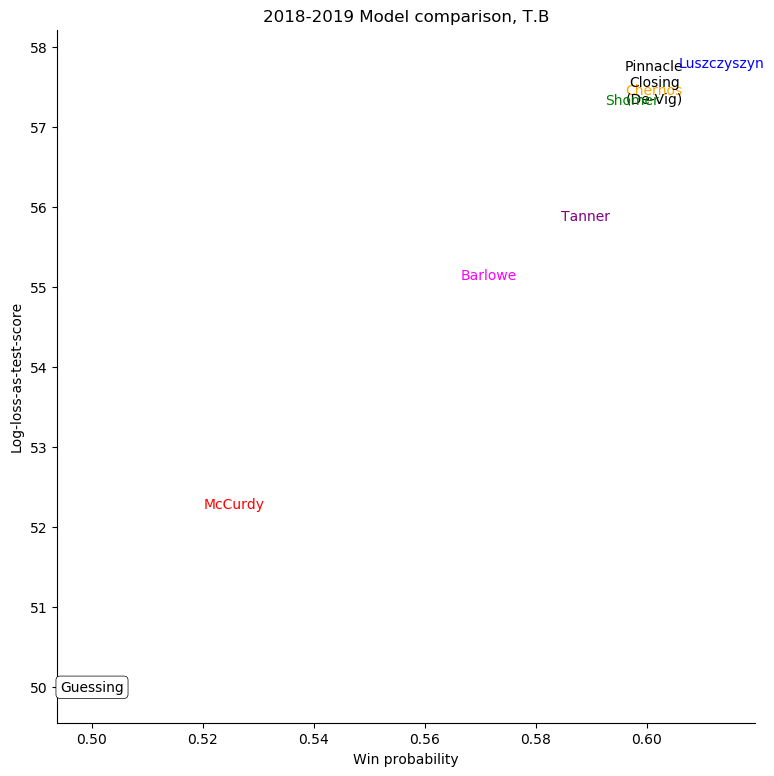
Team-by-team Results

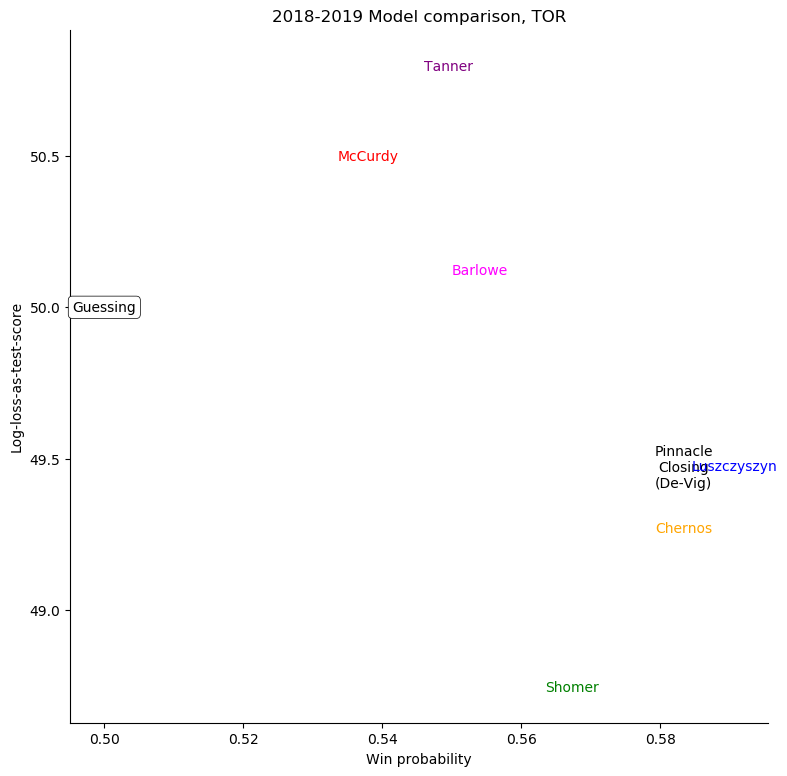
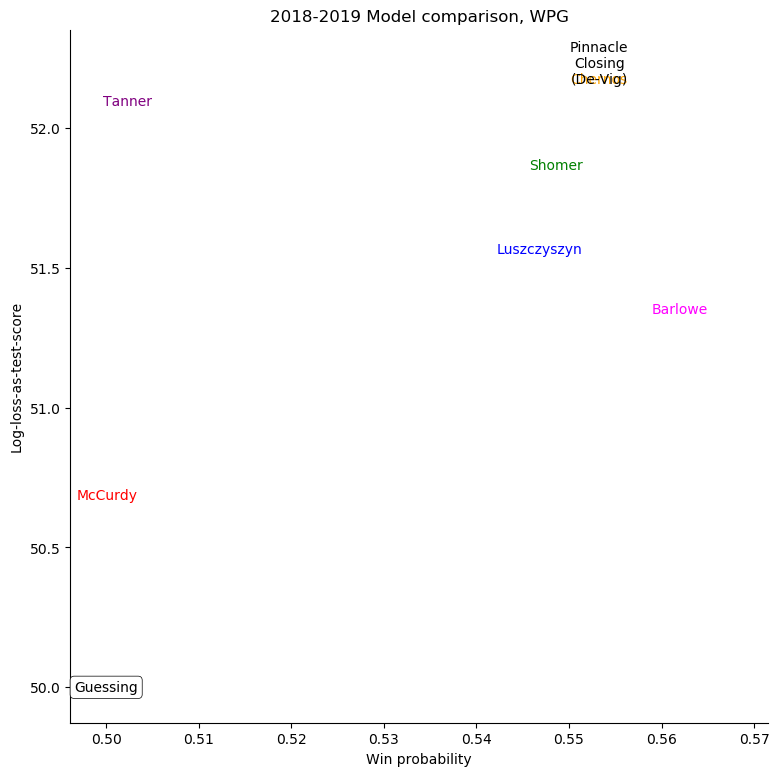
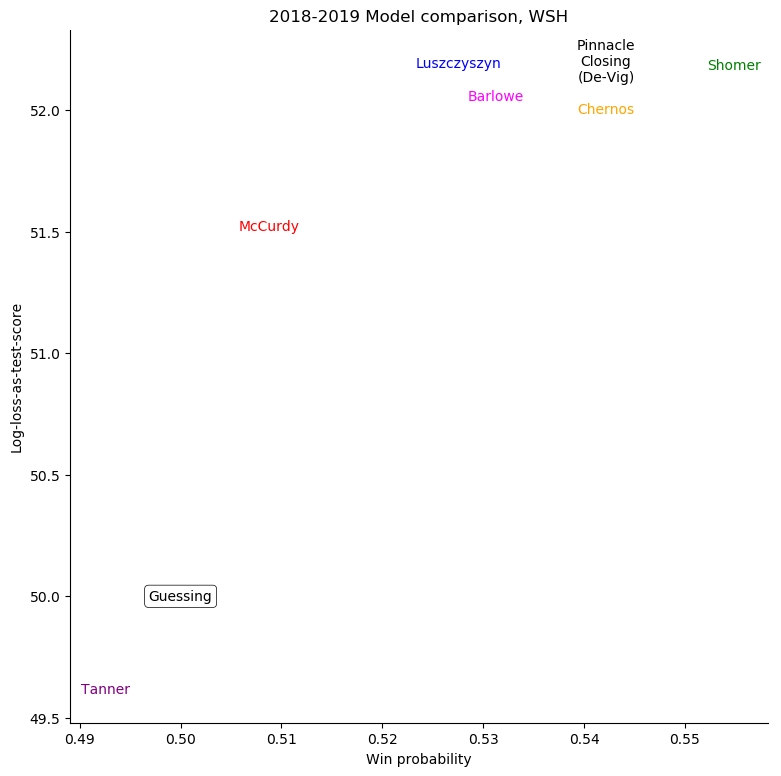
The same exercise can be repeated for each individual team, shown in the table below.

For some very successful teams, like Boston or Tampa, an easy way to score highly was to back them very strongly. For other, very unsuccessful teams, like Anaheim, Detroit, Los Angeles, or Ottawa, the easy way to score highly was to strongly back their opponents. Most other teams don't show a clear "underrate"/"overrate" pattern.

---