Introduction
In addition to trying to score during their shifts, hockey players can help their teams in another way: by leaving the puck farther up the ice at the end of their shift than it was when they came on the ice. Conversely, players can hurt their teams immediately by conceding goals but can also simply lose ground, making life harder for their teammates and coach. Here I provide a framework for measuring this secondary effect on ice position by examining how players cause (or fail to cause) the puck to move across the two blue-lines.
This research was first presented at the Ottawa Hockey Analaytics Conference in 2021, for which both slides and video are available; some small improvements have been made since then.
Overview
Every second that the puck is in play, it is contested. All five players from both teams usually work together to move the puck from wherever it is to a place closer to their opponent's goal—exceptions to this generality are usually dramatic enough to be memorable.
The offside rule (where players without the puck must cross the blueline after the puck) divides the rink into three zones. I am interested in measuring the impact of each skater on the movement of the puck across both bluelines. Since every transition is desired by one team and undesired by the other, there are four impacts to measure:
- How a player affects exit offence, that is, moving the puck from their own zone into the neutral zone.
- How a player affects entry offence, that is, moving the puck from the neutral zone into their opponent's zone.
- How a player affects exit defence, that is, keeping the puck in their opponent's zone.
- How a player affects entry defence, that is, keeping the puck out of their own zone.
Method
Strictly speaking I measure these impacts with two different but heavily overlapping models.
- The entry model has two observations for every second of five-on-five play during which the puck is in the neutral zone. Every second of game-time when the puck is in the neutral zone gives rise to two observations, one observation where the home team is considered the "offence" team and the road team the "defence" team, the other observation the other way around. The response variable is set to 1 if the offence team moves the puck into their offensive zone and 0 if they have not.
- The exit model has one observation for every second that the puck is not in the neutral zone. Here the roles of offence and defence are not symmetric as in the entry model; the team playing near their own goalie is the "offence" team (they are the ones trying to take the puck up the ice), the team playing far from their goalie is the "defence" team; while they are obviously trying to score they are simultaneously defending the blue line immediately behind them, which is the sense that applies for my purpose today.
Furthermore, each team's head coach is included in each of the four senses, to proxy for how they instruct (either directly or indirectly) their players to play.
Both models also share the following additional terms:
- Seven terms for the current score in the game:
- Trailing by three or more;
- Trailing by two;
- Trailing by one;
- Tied
- Leading by one;
- Leading by two;
- Leading by three or more.
- Three terms for the period of the game
- Two terms for home/road
- Three interaction terms for the game states in which teams conventionally
change their tactics:
- Tied in the third period;
- Leading by one in the third period;
- Leading by two in the third period.
I am interested in transitions for three different reasons. Most importantly, I want to obtain the coefficients for the non-player terms in order to understand the sport better. Second, I want to obtain the estimates for the player terms in order to understand how they obtain the more important on-ice impacts (such as shots and goals) on the game that they do. Finally, I want to measure the off-ice impact that players can have on the shifts which follow theirs, by leaving the puck in more (or less) promising locations than when they begin their shifts.
Fitting
This model is fitted as a logistic regression, with three kinds of ridge penalties, similar to my shot rate model. One penalty (of strength 100) is applied to every non-constant term's deviation from zero, to encode our prior intuition that no one player or structural term can dramatically change on-ice results by themselves. A second penalty (also of strength 100) is applied to every term's deviation from its value in the previous season, encoding our prior belief that the players and the sport itself change slowly over time. Finally, a third penalty (of strength 100 million) is used to pool the score terms to enforce our knowledge that all the score effects taken together must average to zero.
Structural Results
As always, the coefficients from a logistic regression are a bit of a pain to interpet. Positive values are associated with players or structural effects that make transitions more likely, and negative values with ones who make transitions less likely. In order to make them a little easier to understand, I've decided to quote them after transforming them somewhat. Each transition (entry or exit) has an associated constant term; converting this to a probability gives the chance of a transition in a given second assuming all other factors have no effect. This probability can be innverted to give an average time until the transition occurs. Repeating this process with the constant and a given term added lets us compare the two, to quote the effect of that term in seconds. One player might delay the mean time until their team exits their zone by five seconds, another structural term might icrease that time by four seconds, on average, say. These changes, strictly speaking, cannot be added together, but they give a certain naturality.
We'll return to the player and coach terms in time, but let's start with the structural terms. First, exits in 21-22:

We know that trailing teams usually dominate in shots and we see the same here for transitions. Trailing is associated with shaving around two seconds off the time it takes to get the puck out of your own zone and leading by one or two adds about a second. Teams that are up a lot are downright leisurely getting the puck out. Similarly, zone exits come quicker early in the game and slower in the third; the interaction terms between leading and the third period are also very strong; this is the environment where score effects are strongest. Road teams have a roughly two-second harder time exiting their zone than home teams.
For entries in 21-22:
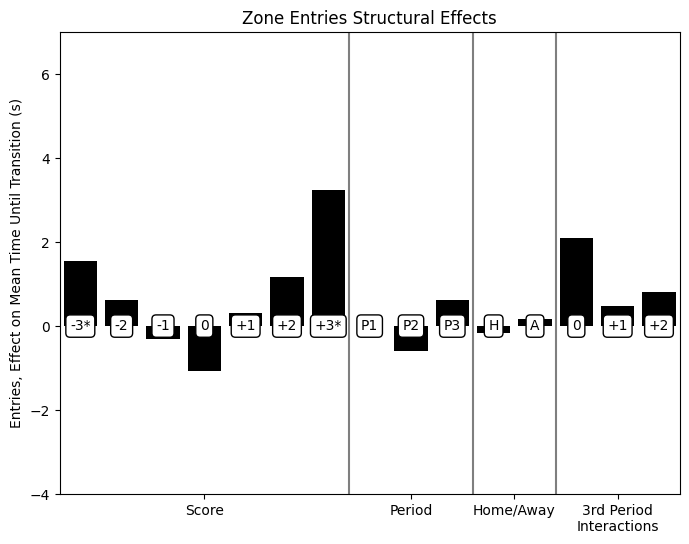
When the puck is in the neutral zone, the impact of the score is quite different: tied games are the ones where entries are a little easier to come by, and both leading and trailing are associated with longer time until entry. Leading teams gaining the neutral zone and then dumping the puck and changing is familiar enough behaviour. Trailing teams having an easier time getting out of their own zone and also a harder time getting into the offensive zone suggests that leading teams systematically drop back, preferring to defend their own blue line better than their opponent's.
The period and home/road terms are very small, and the third-period interaction effects are also quite small, except for the "when tied" term. Games which are tied-in-the-third specifically have clogged neutral zones. The year-to-year variation in the structural terms is small.
Skater Results
Coefficients
Results for individual skaters are organized by team, although the coefficients shown are for the player's results on all teams for which they played in the given season. For context, each team's results are shown on a blue density which shows the distribution of all of the skaters in the league in that year. The correlations indicated in the titles are the correlation of the offence value to the defence value for the whole league. As you will notice, entry offence is strongly correlated with entry defence, but exit offence is not strongly correlated with exit defence.
For completeness' sake, I've presented the four terms for each skater in four different ways:
- D: Entry Defence vs Exit Defence
- O: Entry Offence vs Exit Offence
- N: Entry Offence vs Entry Defence
- X: Exit Offence vs Exit Defence
The first row shows the coaching terms; they are much smaller in magnitude but their effect is felt on every entry or exit.
Off-ice Impacts
The structural terms tell us something about the sport itself; the coaching and player terms give us insight into player evaluation and how players achieve their on-ice shot rate impacts. However, we can use the same information to measure another aspect of player performance, that is, which players are gaining ice position and which are losing ground? Every time a coach makes a line change, they must give out shift start to the new players based on whatever the previous players have done; some players create zone start "currency" for their teammates and others spend it. Using the coefficients above for each player, we can estimate this impact also.
Let us form a matrix of "league-average" transition probabilities, as follows: $$ T = \begin{bmatrix} \textrm{D to D} & \textrm{D to N} & \textrm{D to O} \\ \textrm{N to D} & \textrm{N to N} & \textrm{N to O} \\ \textrm{O to D} & \textrm{O to N} & \textrm{O to O} \\ \end{bmatrix} $$ Since transitions from the offensive zone immediately to the defensive zone (or vice/versa) without the puck passing through the neutral zone are very uncommon (caused only by penalties), let us set those terms to zero: $$ T = \begin{bmatrix} \textrm{D to D} & \textrm{D to N} & 0 \\ \textrm{N to D} & \textrm{N to N} & \textrm{N to O} \\ 0 & \textrm{O to N} & \textrm{O to O} \\ \end{bmatrix} $$
By converting the constant terms of the entry regression and the exit regression into probabilities, we can compute the off-diagonal terms as follows: $$ T = \begin{bmatrix} \textrm{D to D} & 2.5\% & 0 \\ 6.5\% & \textrm{N to N} & 6.5\% \\ 0 & 2.5\% & \textrm{O to O} \\ \end{bmatrix} $$ For a specific player, we can compute the transition probabilities again, using only the constant term and their impact. For instance, for a given (imaginary, very strong) player \(p\) we might have $$ T_p = \begin{bmatrix} \textrm{D to D} & 3.2\% & 0 \\ 6.1\% & \textrm{N to N} & 6.9\% \\ 0 & 2.1\% & \textrm{O to O} \\ \end{bmatrix} $$ Since the rows of a transition matrix must sum to 1, we can compute the missing terms as: $$ T_p = \begin{bmatrix} 1-3.2\% & 3.2\% & 0 \\ 6.1\% & 1-6.1\%-6.9\% & 6.9\% \\ 0 & 2.1\% & 1-2.1\% \\ \end{bmatrix} = \begin{bmatrix} 96.8\% & 3.2\% & 0 \\ 6.1\% & 87.0\% & 6.9\% \\ 0 & 2.1\% & 97.9\% \\ \end{bmatrix} $$ This transition matrix gives the per-second probability of a given transition. Systems governed by such transition matrixes fairly quickly reach their steady states, which can be computed by taking a higher power of \(T_p\); we can use this steady state matrix to estimate the impact of a player on ice position after a full shift. In this case, $$ T_p^\infty = \begin{bmatrix} 30.8\% & 16.1\% & 53.1\% \\ 30.8\% & 16.1\% & 53.1\% \\ 30.8\% & 16.1\% & 53.1\% \\ \end{bmatrix} $$ So, given a decent stretch of icetime with league-average starting deployment, our player \(p\) can expect to be found with the puck in the defensive zone 30.8% of the time, in the neutral zone 16.1% of the time, and in the offensive zone 53.1% of time; this imaginary player \(p\) is gaining ice position, a fair bit. How much is this gain in ice position worth?
In order to compare this off-ice impact with on-ice impact, we can weight this steady state vector by the measured impact of starting a shift in each of the three zones, taken from my shot rate model. A typical recent deployment for shift starts is 10.3% DZ shift starts, 17.5% neutral zone starts, 11.7% offensive zone starts, and 60.5% on-the-fly. Since on-the-fly starts contain relatively large numbers of shots (like in-zone starts and unlike neutral-zone starts), if we choose to artificially divide those starts into offensive zone and defensive zone starts, we have a "notional league average" deployment of 40.5% DZ, 17.5% NZ, 42.0% OZ. (Notice that our hypothetical player \(p\) is still gaining ice position, even relative to the tendancy of coaches to start more shifts for all players in the offensive zone.) Let us call this vector of "standard" deployment \(s\), so we can compute the net gain or loss in territory as \(T_p^\infty s - s\). We would like to find a way to interpret this vector in more familiar units.
The impact of starting a shift in the defensive zone in my shot rate model is -29.4% of league-average xG/60, starting in the neutral zone -24.8% xG/60, in the offensive zone +17.3 xG/60, and on-the-fly +7.4% xG/60. Dividing the on-the-fly impact evenly between the DZ and OZ impact as before, we get impacts of -25.7% xG/60 for DZ, -24.8% xG/60 for NZ, and 21.0% xG/60 for OZ. Let us call this vectors of impacts \(G\).
Finally, with a reference deployment and impacts in hand, we can form the weighted sum of the net change in ice position \(T_p^\infty s - s\) by the impact \(G\) of the following shifts to obtain \((T^\infty_p s - s) \cdot G\), the total net impact of ice position gained or lost in xG/60. For the entire league, this distribution broadly stretches from -1% to +1%; about ten times narrower than the distribution of on-ice impacts. On the one hand, this is quite small in absolute terms; league average xG/60 at 5v5 is around 2.6, so one percent of this is worth about 0.026 goals every sixty minutes. Very roughly, a player near the top of the league in gaining ice position in this sense who plays a lot of minutes can expect to contribute about five goals a season, which is small but non-trivial. Importantly, these goals created by this notional excellent position-gainer will not merely not be scored by that player; they won't even be scored while that player is on the ice.
The player results for this season are summarized for each team here. As before, the value indicated for each player is their impact for the whole season.
| Pacific | Central | Metropolitan | Atlantic |
|---|---|---|---|
ANA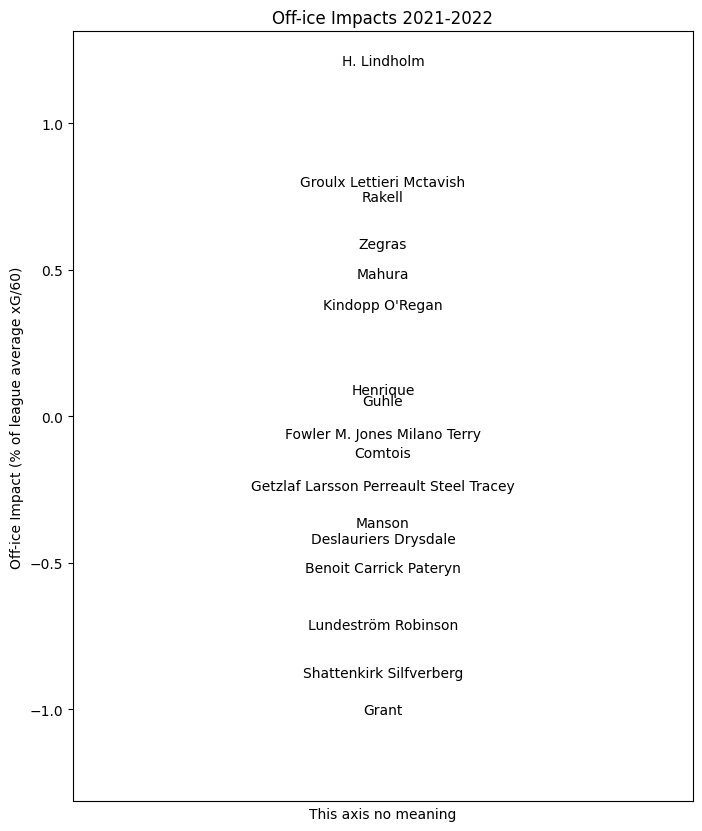
|
ARI
|
CAR
|
BOS
|
CGY
|
CHI
|
CBJ
|
BUF
|
EDM
|
COL
|
N.J
|
DET
|
L.A
|
DAL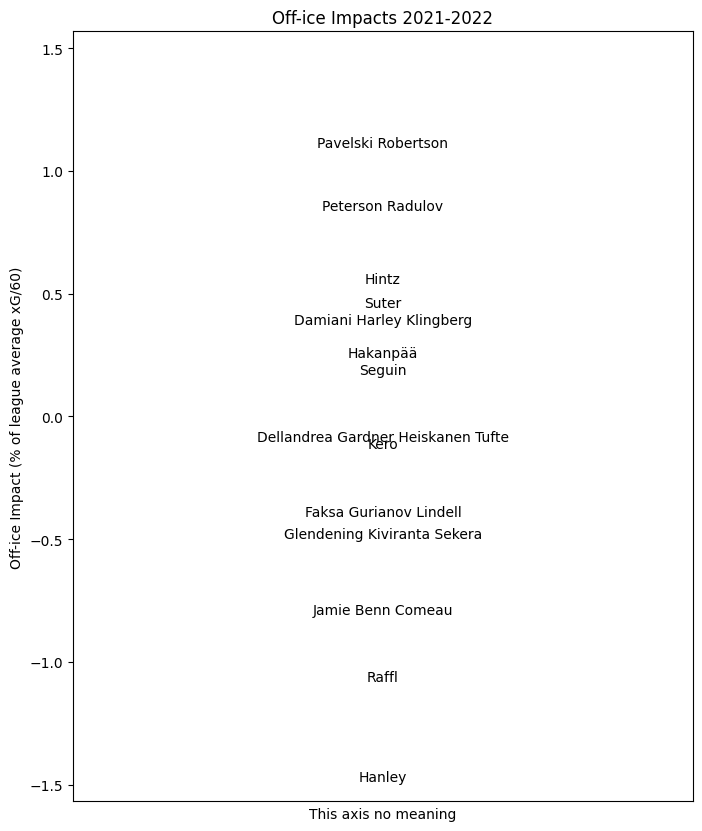
|
NYI
|
FLA
|
S.J
|
MIN
|
NYR
|
MTL
|
SEA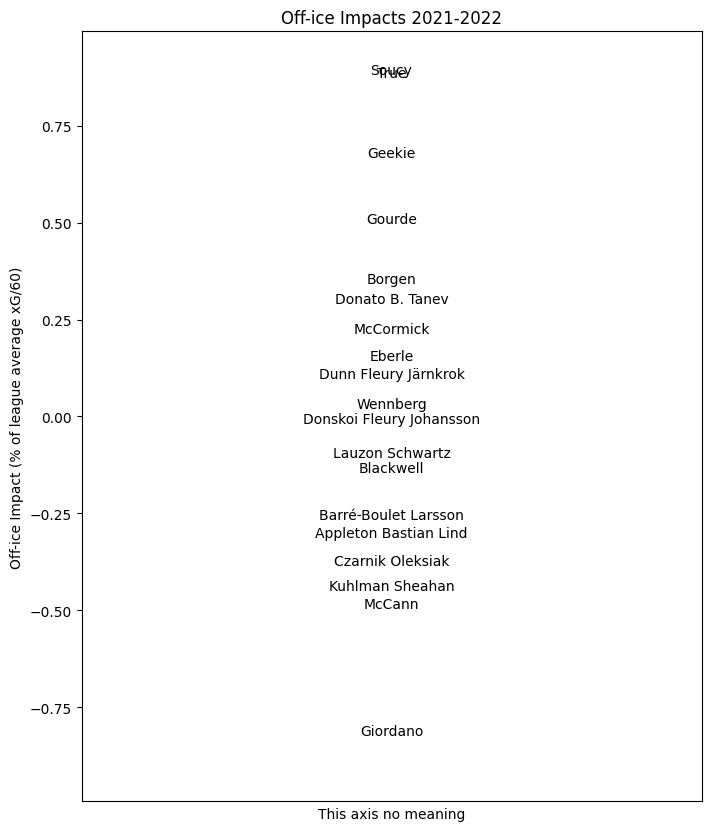
|
NSH
|
PHI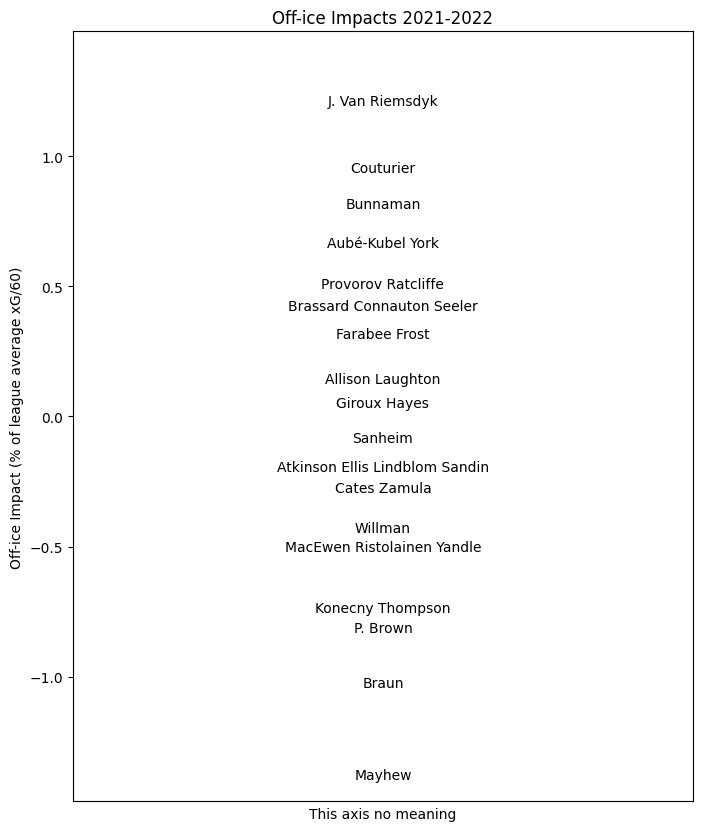
|
OTT
|
VAN
|
STL
|
PIT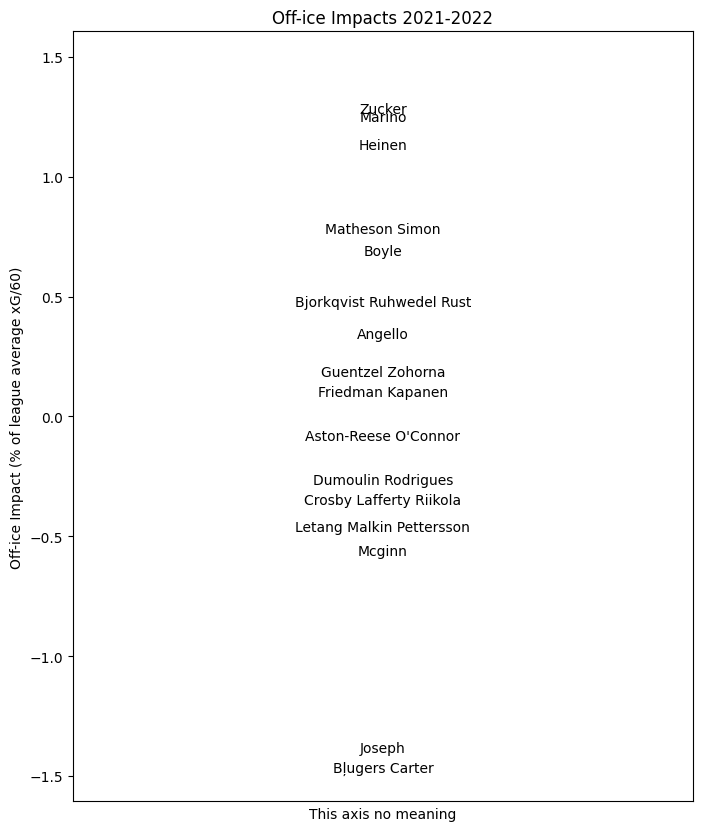
|
T.B
|
VGK
|
WPG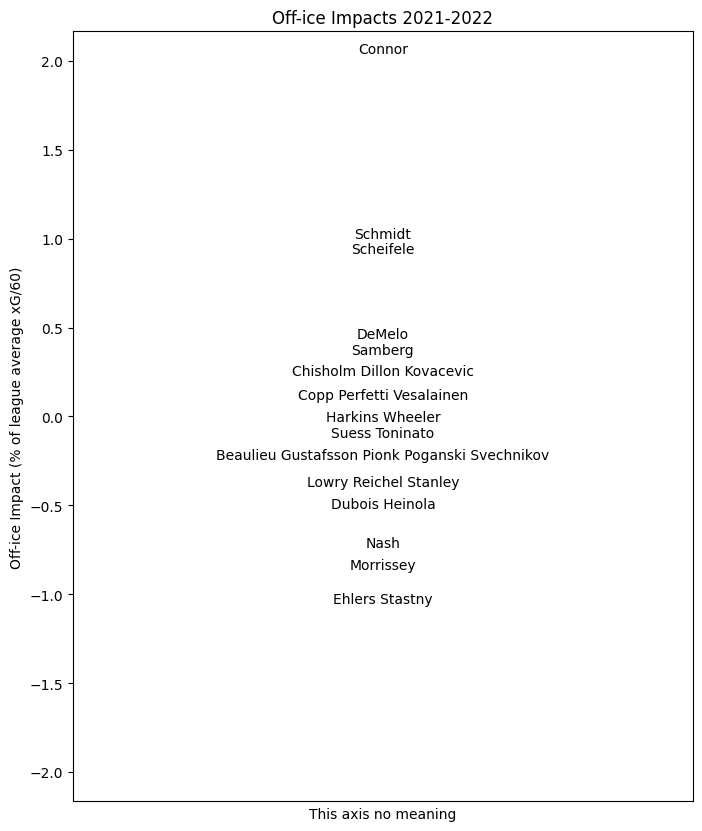
|
WSH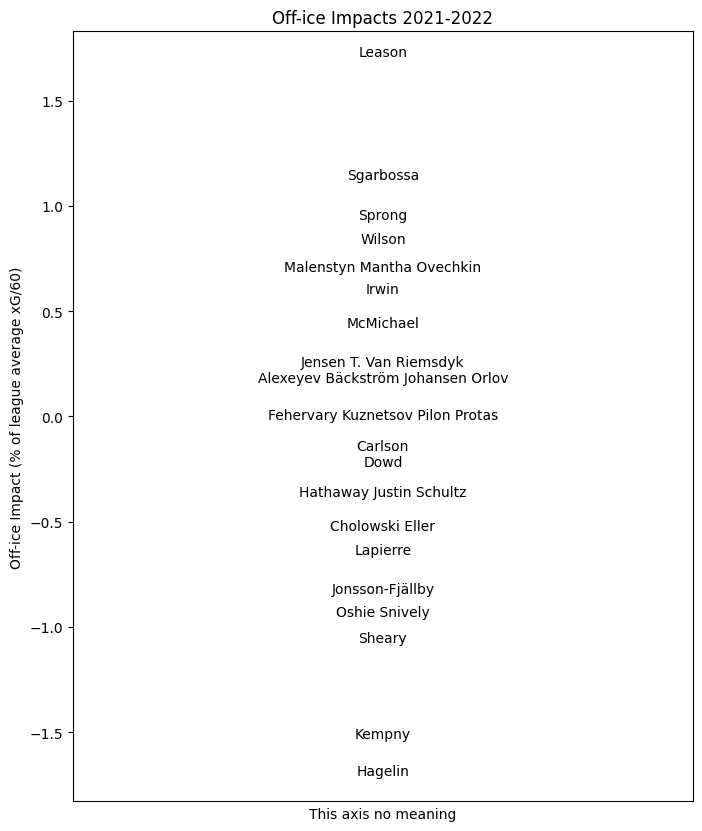
|
TOR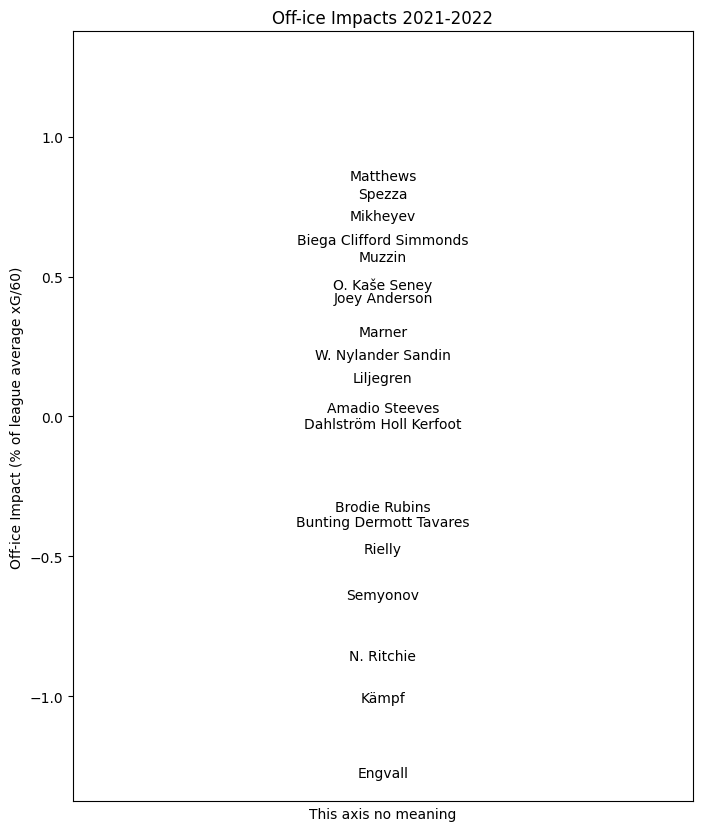
|
Weaknesses
I have deliberately chosen to work with the nhl's public play-by-play data, from which the puck location at many (but not all) times can be imputed. However, there are times when the puck moves from a defensive zone into the neutral zone and then back into that same defensive zone without an event being recorded; my approach here will treat this as a continuous stretch of play in the defensive zone. The effect of these omissions will tend to make players and coaches look worse at zone exits and better at entry defence. Similarly, there are some number of zone entries which are followed by a return of the puck to the neutral zone without any record; these omissions will tend to make coaches and players stronger at entry defence and weaker at zone exits than they actually are. I don't know how to estimate how common these two omissions are in order to even guess at a comparison between these two effects.